Circle Square Hybrid
Consider a unit circle centered on the origin, and a circumscribing square. We could represent these curves in polar coordinates as ( R 1 ( θ ) , θ ) and ( R 2 ( θ ) , θ ) .
Form a third curve as follows:
R 3 ( θ ) = 2 R 1 ( θ ) + R 2 ( θ )
What is the area enclosed by the third curve? Note that this is the combined area of the tan and blue regions. If this area is A , give your answer as ⌊ 1 0 0 0 A ⌋ , where ⌊ ⋅ ⌋ denotes the floor function.
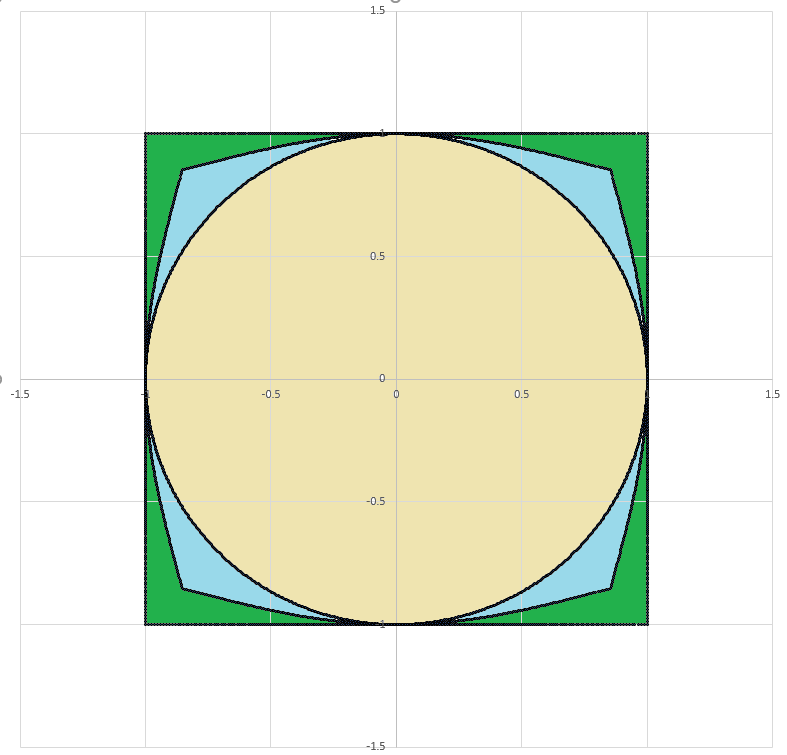
The answer is 3548.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Similar solution with @Aaghaz Mahajan 's
We note that R 1 ( θ ) = 1 and R 2 ( θ ) = cos θ 1 = sec θ . Then R 3 ( θ ) = 2 R 1 ( θ ) + R 2 ( θ ) = 2 1 + sec θ , and the area enclosed by R 3 ( θ ) :
A = ∫ 0 2 π 2 1 R 3 2 ( θ ) d θ = 8 ∫ 0 4 π 2 1 R 3 2 ( θ ) d θ = ∫ 0 4 π ( 1 + sec θ ) 2 d θ = ∫ 0 4 π ( 1 + 2 sec θ + sec 2 θ ) d θ = ∫ 0 4 π d θ + 2 ∫ 0 4 π sec θ d θ + ∫ 0 4 π sec 2 θ d θ = [ θ + 2 ∫ tan θ + sec θ tan θ sec θ + sec 2 θ d θ + ∫ d tan θ ] 0 4 π = [ θ + 2 ln ( tan θ + sec θ ) + tan θ ] 0 4 π = 4 π + 2 ln ( 1 + 2 ) + 1 ≈ 3 . 5 4 8 1 4 5 Since R 3 ( θ ) is symmetrical about the origin
Therefore, ⌊ 1 0 0 0 A ⌋ = 3 5 4 8 .
We know that
R 1 = 1 and R 2 = sec θ { − 4 π ≤ θ ≤ 4 π } denotes the right vertical edge of the square. Now,
R 3 = 2 ( 1 + sec θ ) { − 4 π ≤ θ ≤ 4 π } for the right bulging side of the third curve. Now, we simply calculate the area of this part and multiply it by 4 since the figure is symmetrical.
Hence, we get area of one part
8 1 ∫ − 4 π 4 π ( 1 + sec θ ) 2 d θ
= 8 1 ( 2 π + 4 ln ( 2 + 1 ) + 2 )
Hence, total area of the third curve is
4 π + 2 ln ( 2 + 1 ) + 1 = 3 . 5 4 8 1 4 . . . .