Circle squared
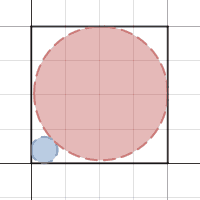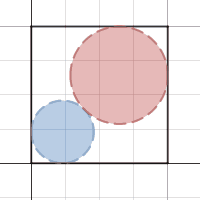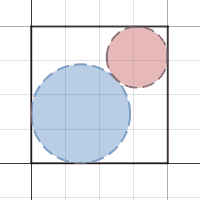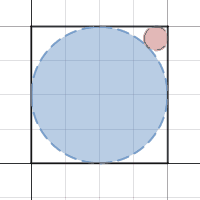 Consider a square
A
B
C
D
. Two circles
X
and
Y
are drawn such that circle
X
is tangent to two adjacent sides
A
B
and
A
D
, and circle
Y
is tangent to the other two adjacent sides
C
B
and
C
D
,
and circles
X
and
Y
are tangent to each other.
Consider a square
A
B
C
D
. Two circles
X
and
Y
are drawn such that circle
X
is tangent to two adjacent sides
A
B
and
A
D
, and circle
Y
is tangent to the other two adjacent sides
C
B
and
C
D
,
and circles
X
and
Y
are tangent to each other.
As the radius of circle X increases, at what radius of circle X does the sum of the areas of circle X and Y change the slowest?
Express that radius as a fraction of the side of the square A B C D , and round to the nearest hundredth.
The answer is 0.29.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
I just used logic to solve. The only place where we can get uniqueness is when the circles are the same size, otherwise, they are mirror images of each other. So I just solved for the radius at that point :). Actually I'm posting this to ask if it is 'fair' to use this sort of reasoning. I did it to save time
Log in to reply
I thought about that, but I couldn't convince myself it was anything more than a coincidence. I don't see why, a priori, it couldn't be the fastest change when one circle had zero radius, or one circle was twice as big as the other, or some other ratio.
It does happen to be true in this circumstance, but I wouldn't say in general that if a problem contains only one unique point, that point must be directly involved in the solution.
Log in to reply
Yes, I agree with you all. But the question asked specifically about the radius on X. And since the two circles are absolutely the same at some points, if there's such a position on circle X, there would be another one on circle Y at one point and this goes on and on. The only place both of them will be satisfied is where they meet. If the question had asked for a ratio of the smaller and bigger circle, then I would be stumped. I hope I make sense. I'm an engineer and I only do math for fun. I don't have the vocabulary like y'all
My initial guess before working on the problem was the "symmetry solution" you describe, which more often than not is correct. But just as Brian Kardon notes, I couldn't convince myself that this was going to necessarily be the case here, so I proceeded with my analysis. If you're short of time and need to make an educated guess, though, your intuitive approach is good, but would not constitute a proof. :)
The solution need not be unique. For example, if the "area" had the form ( a − 4 1 ) 2 ( b − 4 1 ) 2 subject to a + b = 1 , then the minimum would occur at 2 places.
My approach is similar to Brian's.
Denote the radii by r and R and note that r + R = 2 − 2 , so that we can write r and R as 2 2 − 2 ± d and π A = r 2 + R 2 = 2 ( 2 − 2 ) 2 + 2 d 2 . The minimum is attained when d = 0 and r = R = 2 2 − 2 ≈ 0 . 2 9 . At that point, the rate of change of the A is 0.
In my opinion Olawale Olayemi is right I took this approach considering :
1) The solution must be in a point where the function representing the sum of areas of circles is a maximum or a minimum since her derivative must be 0.
2) Assuming two solution exist, by symmetry we must have two points where derivative is 0 and second derivative must have same value and sign that should force to the existence of another points in between where derivative must equal 0, against hypothesis. Therefore equal radii circles is the only solution.
Without loss of generality let the square be a unit square. Let the blue circle, aka circle X , have radius r and the red circle, aka circle Y , have radius R . Then the diagonal of the unit square can be divided into 4 sections: one each of the radii of the two circles and one each of the diagonals of squares with side lengths r and R . This results in the equation
r ( 1 + 2 ) + R ( 1 + 2 ) = 2
⟹ r + R = 1 + 2 2 = 2 − 2 ⟹ R = ( 2 − 2 ) − r .
The combined area A of the two circles is then
A = π r 2 + π R 2 = π ( r 2 + ( ( 2 − 2 ) − r ) 2 ) =
2 π ( r 2 − ( 2 − 2 ) r + ( 3 − 2 2 ) ) .
Now d r d A = 2 π ( 2 r − ( 2 − 2 ) ) = 0 when r = 2 2 − 2 , so the magnitude of the change in A is least when circle X has this radius. For this value of r we see also that R = r , i.e., the change in A is least when the two circle have the same radius.
Thus, as this value for r was obtained for a unit square, the desired fraction is 2 2 − 2 = 0 . 2 9 to the nearest hundredth.