Circle Stacking Sangaku
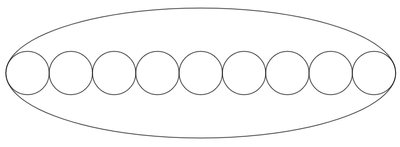
In the ellipse, where the length of the major axis is , and the length of the minor axis is , we can position identical circles along the major axis, such that only two circles each intersect the ellipse once.
Can we do better than that by decreasing the number of identical circles while increasing their areas?
Also try the sister problem I posted.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The radius of curvature of the ellipse at the end point is 6 5
The radius of the circles if there are 8 of them will be 1 6 1 5 which is greater than the radius of curvature of the ellipse and hence will bulge outside of the ellipse