Circle surrounded by many circles!
Geometry
Level
3
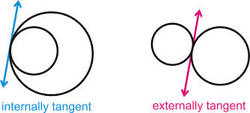 You are given of a circle with radius r. How many possible externally tangent circles to the given circle can you create if their individual radius is half of the given circle.
You are given of a circle with radius r. How many possible externally tangent circles to the given circle can you create if their individual radius is half of the given circle.
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
the circumference of outer circle is: 2 π ( r + 2 r ) = 3 π r since circles touch each other diistance between points of contact is r = r/2 + r/2; Hence 3 π = 9 such circles can be joined together.