Circle Tangent to a Parabola?
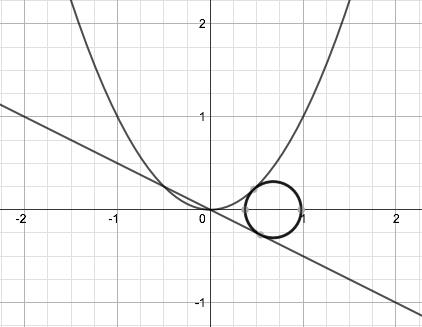 The above picture shows the graphs of the parabola
y
=
x
2
and the line
y
=
−
2
1
x
in Cartesian coordinates. A circle with center
(
p
,
0
)
, where
p
>
0
, is tangent to both the parabola and the line. What is the value of
p
rounded to three decimal places?
The above picture shows the graphs of the parabola
y
=
x
2
and the line
y
=
−
2
1
x
in Cartesian coordinates. A circle with center
(
p
,
0
)
, where
p
>
0
, is tangent to both the parabola and the line. What is the value of
p
rounded to three decimal places?
Graph generated in Desmos .
The answer is 0.677.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Hello Ronak Agarwal, that's a very good solution. However, I also tried solving it using a different approach and I got the final answer as 6 4 8 3 0 + 1 3 0 6 5 which has the same value as your answer but in a different form. Can you please guide me on how to convert my answer into this form? f ( a + b ) ( − c + d e ) Thank you very much.
Log in to reply
actually the question has been wrongly asked i did get same and also converted it but the answer i received was different check this (8+sqrt(65))(sqrt(-28130+3490sqrt(65))/64
We have the centre of the circle as A = ( x , 0 ) let the point of contact of circle and parabola be B = ( t , t 2 ) .
Ist equation we would be writing is that the tangent and AB is perpendicular to each other, hence we write :
( S l o p e o f t a n g e n t ) ( S l o p e A B ) = − 1
( 2 t ) ( t − x t 2 ) = − 1
rewriting it we have :
2 t 3 + t = x Equation 1
Second equation we would be writing is that :
length(AB)=Perpendicular distance from the line x + 2 y = 0
⇒ t 4 + ( t − x ) 2 = 5 x 2 Equation 2
Solving these two equations we get :
x = 1 2 8 ( 1 5 + 6 5 ) ( 2 6 5 − 2 )