Circle the Drain
A triangle has sides 10,17 and altitude 8 through the vetex common to both sides. Find the area of another triangle formed when the centers of following circles are joined (as shown in the figure above):
-
The Incircle.
-
The Circumcircle.
If the answer can be written as a + n m , where a , m and n are positive integers, m < n and m and n are coprime. Find a + m + n .
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
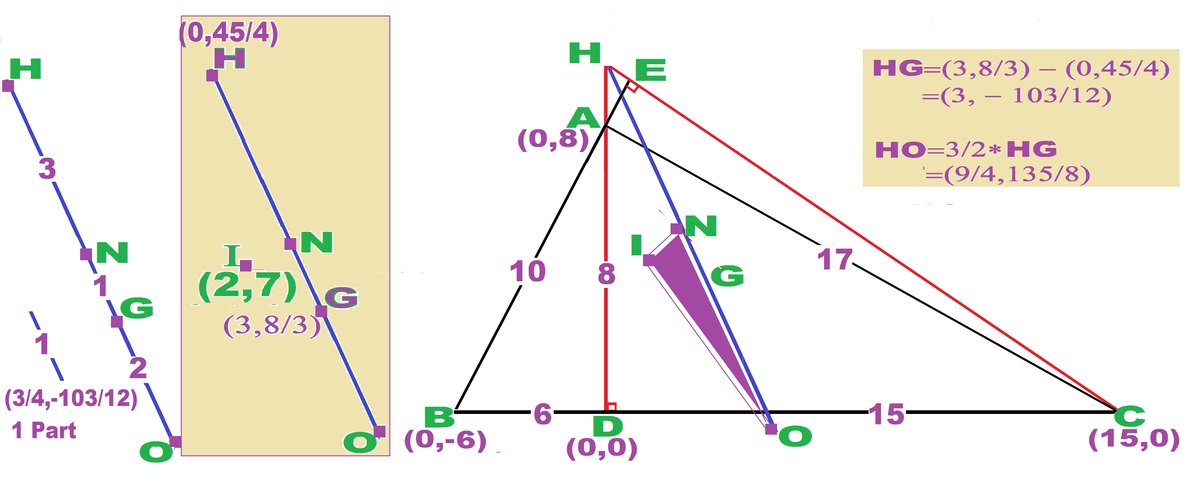
ABC is the triangle with D as the foot of altitude from A. HNGO is a section of Euler Line in blue. H - Orthocenter, N - Nine point center, G - Centroid, O - Circumcenter, I - Incenter. We use coordinate geometry and find coordinates of N, I, O. Coordinate of I is found as . X I = s a X A + b X B + c X C , Y I = s a Y A + b Y B + c Y C To simplify calculations, coordinate axis is chosen taking D as origin, and BC along X-axis. So A(0,8), B(-6,0), C(15,0), a, b, c are sides of ABC. From Pythagoras, BD=6, DC=15. 2 ∗ s = a + b + c = 2 1 + 1 7 + 1 0 , ∴ s = 2 4 . 2 4 ∗ X I = 2 1 ∗ 0 + 1 7 ∗ ( − 6 ) + 1 5 ∗ 1 0 = 4 8 , 2 4 ∗ Y I = 2 1 ∗ 8 + 1 7 ∗ 0 + 1 5 ∗ 0 = 1 6 8 . I ( 2 , 7 ) . In Euler Line, if we know two points, we can find out other points. It takes less calculations to find G and H, since we know coordinates of A, B, C, one altitude AD, can easily find slope of CH. ⟹ X G = 3 0 − 6 + 1 5 = 3 , Y G = 3 8 + 0 + 0 = 3 8 . G ( 3 , 3 8 ) . CE is the altitude from C, to meet BA extended at E, extended further to H to meet DA extended . Y B A = 6 8 X + 8 . C E ⊥ B A , ⟹ Y C E − 0 = 8 − 6 ( X − 1 5 ) , ⟹ Y C E = 4 − 3 ∗ X − 4 4 5 . So H on X=0, is H ( 0 , 4 4 5 ) . Properties of Euler Line. O H = 2 3 ∗ G H = 2 3 ∗ { G − H } = 2 3 ∗ { ( 3 , 3 8 ) − ( 0 , 4 4 5 ) } = ( 2 9 , 4 − 4 ∗ 2 4 5 ∗ 3 ) ∴ H + O H = ( 2 9 , 4 − 4 ∗ 2 4 5 ∗ 3 + 4 4 5 ) = ( 2 9 , 4 − 4 ∗ 2 4 5 Will come soon to complete .
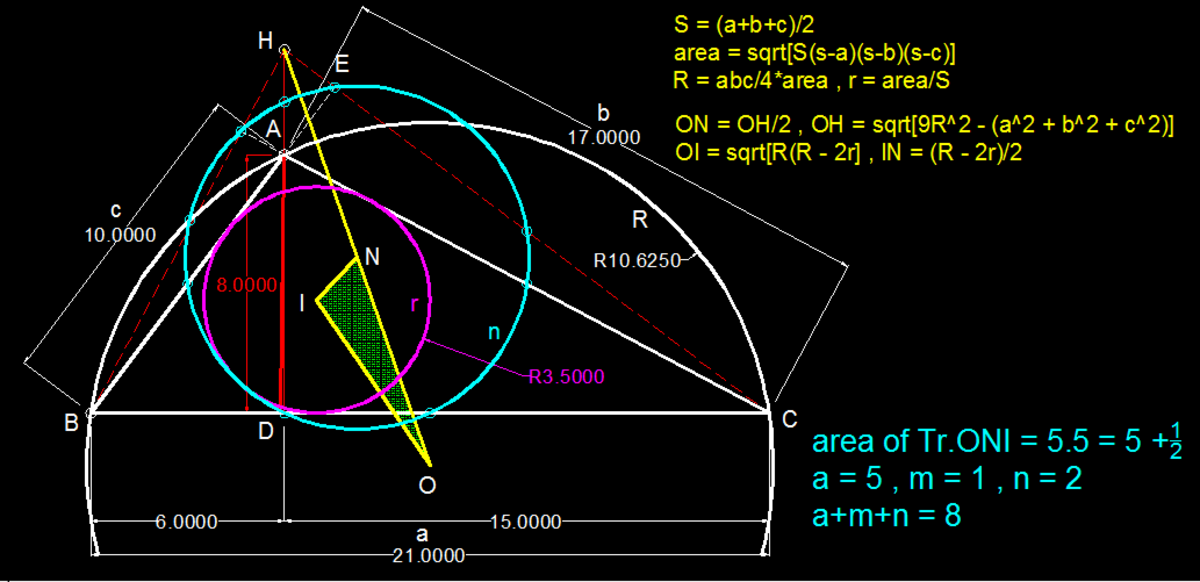
This question was very long (at least by my method).
I used coordinate geometry.
After lots of calculations I arrived at the following conclusion. (See image below)
In the given image I denotes the incenter , C denotes the cicumcenter and N denotes the center of nine point circle.
Now we could have just figured out the area by area formula.