Circle : Triangle
Two circles are placed in an equilateral triangle as shown in the figure. What is the ratio of the area of the smaller circle to that of the equilateral triangle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
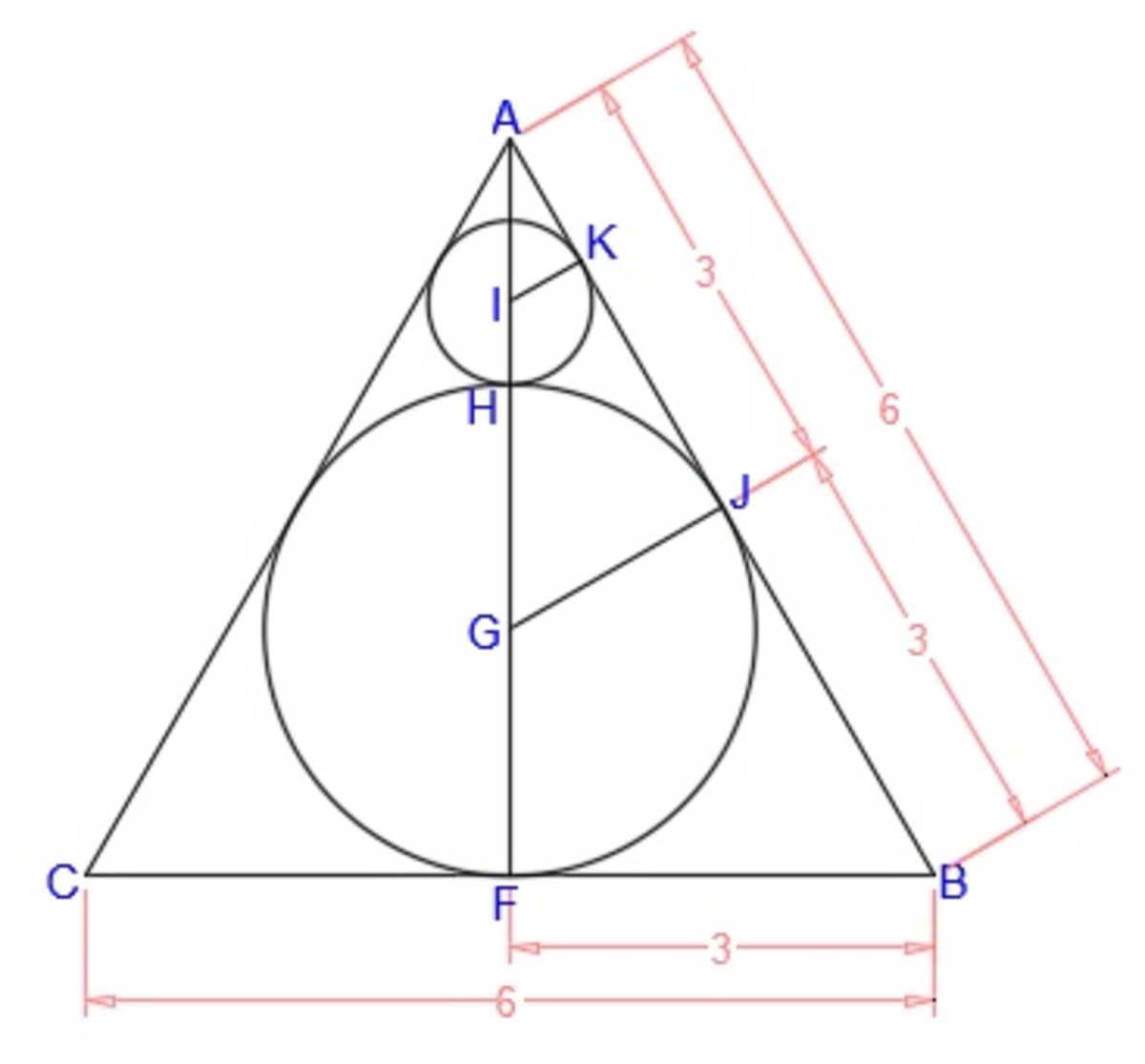 Let the side length of the equilateral triangle be
6
, then by pythagorean theorem,
A
F
=
6
2
−
3
2
=
2
7
=
3
3
.
Let the side length of the equilateral triangle be
6
, then by pythagorean theorem,
A
F
=
6
2
−
3
2
=
2
7
=
3
3
.
Since △ A J G ∼ △ A F B , we have A J J G = A F F B ⟹ 3 J G = 3 3 3 ⟹ J G = 3 = G F .
H F = J G + G F = 3 + 3 = 2 3
A H = A F − H F = 3 3 − 2 3 = 3
Let K I = H I = r .
A I = A H − r = 3 − r
Since △ A K I ∼ △ A J G , we have
J G r = A G A I ⟹ 3 r = 2 3 3 − r ⟹ 2 3 r = 3 − 3 r ⟹ 3 3 r = 3 ⟹ r = 3 1
So the area of the small circle is π r 2 = π ( 3 1 ) 2 = 3 π and the area of the equilateral triangle is 4 3 ( 6 2 ) = 9 3 .
The desired ratio is 9 3 3 π = 2 7 3 π .
Marvin has given a good solution. I would like to provide an alternate solution that would be time efficient . Let the side length of △ A B C = a units
Simply draw a common tangent D E to both circles that touches them at F . We observe that D E ∥ B C .
Though I will not go into the rigour of proving established theorems for what I am about to type, you can do so for your own clarity: we observe that △ A D E is also an equilateral triangle and A G F O I is a straight line.
Also observe that the bigger circle is the in-circle of the equilateral △ A B C . This makes O the centroid and A O the radius of the circumcircle, if it were drawn.
Hence, radius of bigger circle = 2 3 a = O F = O I
A O = 3 a
Now, A F = A O − O F = 3 a − 2 3 a = 2 3 a
Therefore, side length of equilateral △ A D E : A D = D E = E A = 3 a
Observe that the smaller circle is now the in-circle of equilateral △ A D E . So, radius of smaller circle = 6 3 a
Thus, Area of equilateral triangle ABC Area of smaller circle = ( 6 3 ) 2 π a 2 x 3 a 2 4
= 2 7 3 π