Circle Triangle Hybrid
A circle of radius 1 is centered on the origin. An equilateral triangle is inscribed within the circle. Suppose we represent the coordinates of the circle in polar coordinates as ( r c ( θ ) , θ ) , and the coordinates of the triangle as ( r t ( θ ) , θ ) . The polar coordinates specify the position relative to the origin, and the radii vary with θ .
Define a hybrid curve:
r h ( θ ) = 2 r c ( θ ) + r t ( θ )
All three curves are plotted on the diagram below. If the area of the purple region is A , give your answer as ⌊ 1 0 0 0 A ⌋ .
Note: For any particular θ , r c and r t each take on a single positive value
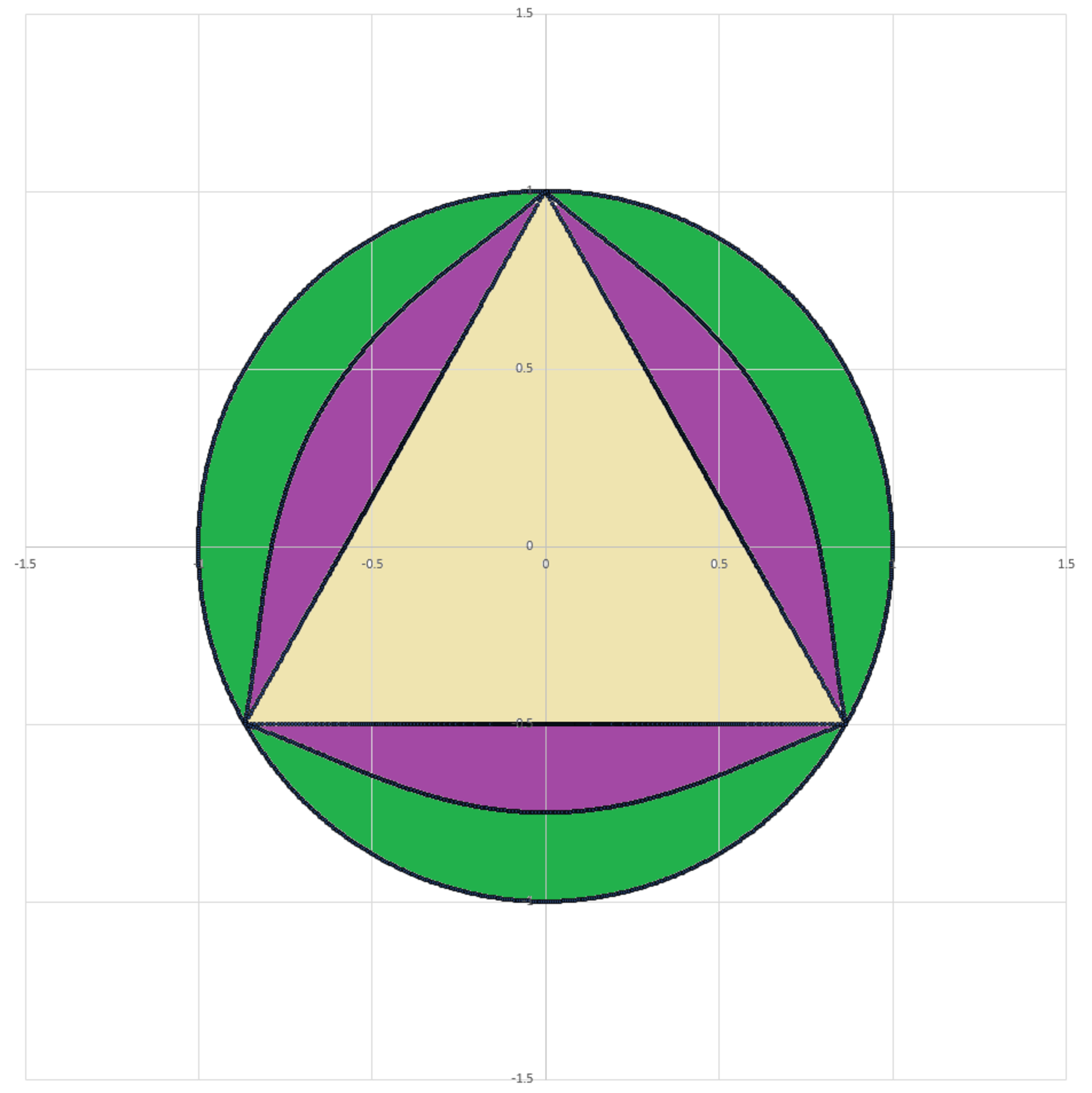
The answer is 798.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Amazing solution, sir! Just a curiosity, are you brazilian too?
Very impressive solution, thanks
The triangle can be parameterised in polar coordinates as such:
r t ( θ ) = ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎧ tan θ + 3 sec θ tan θ − 3 sec θ sin θ − 0 . 5 tan θ + 3 sec θ 0 ≤ θ ≤ 2 π 2 π ≤ θ ≤ 6 7 π 6 7 π ≤ θ ≤ 6 1 1 π 6 1 1 π ≤ θ ≤ 2 π
Finally: the required polar curve is:
r h = 2 r t + 1
And the purple area is computed as such:
A = ∫ 0 2 π 2 1 r h 2 d θ − ∫ 0 2 π 2 1 r t 2 d θ ⟹ A ≈ 0 . 7 9 8 8
Integrals can be solved using any numerical tool.
For the circle:
r c ( θ ) = 1
Let us consider only the right purple area, since the total purple area will be 3 times this one. For the triangle, let us define a straight line from the origin with angle θ with the horizontal. Its equation will be:
y = tan ( θ ) x
The right side of the triangle has equation:
y = − 3 x + 1
So the point of intersection with the triangle (i.e. a generic point in the right side of the triangle) has coordinates:
x = tan ( θ ) + 3 1 , y = tan ( θ ) + 3 tan ( θ )
And then we can calculate r t ( θ ) :
r t 2 ( θ ) = x 2 + y 2 = ( tan ( θ ) + 3 ) 2 tan 2 ( θ ) + 1
r t 2 ( θ ) = ( tan ( θ ) + 3 ) 2 sec 2 ( θ )
r t ( θ ) = tan ( θ ) + 3 sec ( θ )
So:
r h ( θ ) = 2 1 ( tan ( θ ) + 3 sec ( θ ) + 1 )
Let us consider the red marked area in the figure below:
This area will be given by the integral:
∫ − 6 π 2 π 2 1 r h 2 ( θ ) d θ
So the area A p of one purple area will be this integral minus the area of the triangle with legs as the two radii of the circle marked in red in the figure, which make an angle of 3 2 π between them. So, using the area for a triangle knowing two sides and the angle between them:
A p = ∫ − 6 π 2 π 2 1 [ 2 1 ( tan ( θ ) + 3 sec ( θ ) + 1 ) ] 2 d θ − 2 1 ⋅ 1 ⋅ 1 ⋅ sin ( 3 2 π )
A p = 8 1 ⎣ ⎡ ∫ − 6 π 2 π ( tan ( θ ) + 3 ) 2 sec 2 ( θ ) d θ + ∫ − 6 π 2 π d θ + 2 ∫ − 6 π 2 π tan ( θ ) + 3 sec ( θ ) d θ ⎦ ⎤ − 4 3
The first and second integrals are easy to evaluate. On the third, multiplying above and below by cos ( θ ) :
A p = 8 1 ⎣ ⎡ ( ( tan ( θ ) + 3 ) − 1 ) ∣ ∣ ∣ ∣ ∣ − 6 π 2 π + θ ∣ ∣ ∣ ∣ ∣ − 6 π 2 π + 2 ∫ − 6 π 2 π sin ( θ ) + 3 cos ( θ ) 1 d θ ⎦ ⎤ − 4 3
Rewriting the remaining intrgral:
A p = 8 1 ⎣ ⎡ 2 3 + 3 2 π + ∫ − 6 π 2 π 2 1 sin ( θ ) + 2 3 cos ( θ ) 1 d θ ⎦ ⎤ − 4 3
A p = 8 1 ⎣ ⎡ 2 3 + 3 2 π + ∫ − 6 π 2 π cos ( θ − 6 π ) 1 d θ ⎦ ⎤ − 4 3
Make t = θ − 6 π , d t = d θ :
A p = 8 1 ⎣ ⎡ 2 3 + 3 2 π + ∫ − 3 π 3 π sec ( t ) d t ⎦ ⎤ − 4 3
A p = 8 1 ⎣ ⎡ 2 3 + 3 2 π + ln ( sec ( t ) + tan ( t ) ) ∣ ∣ ∣ ∣ ∣ − 3 π 3 π ⎦ ⎤ − 4 3
A p = 8 1 [ 2 3 + 3 2 π + ln ( 2 − 3 2 + 3 ) ] − 4 3
Rationalizing inside the ln :
A p = 8 1 [ 2 3 + 3 2 π + ln ( ( 2 + 3 ) 2 ) ] − 4 3
A p = 1 2 π + 4 ln ( 2 + 3 ) − 1 6 3 3
Since we calculated only one of the 3 purple areas, A = 3 A p :
A = 4 π + 4 3 ln ( 2 + 3 ) − 1 6 9 3 ≈ 0 . 7 9 8 8 3 8
Thus:
⌊ 1 0 0 0 A ⌋ = 7 9 8