Circle can u solve this!
The circle ω touches the circle Ω internally at P. The centre O of Ω is outside ω. Let XY be a diameter of Ω which is also tangent to ω. Assume P Y > P X. Let P Y intersect ω at Z. If Y Z = 2P Z, what is the magnitude of in degrees?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
I am giving a outline, construct and letter the triangle as mentioned,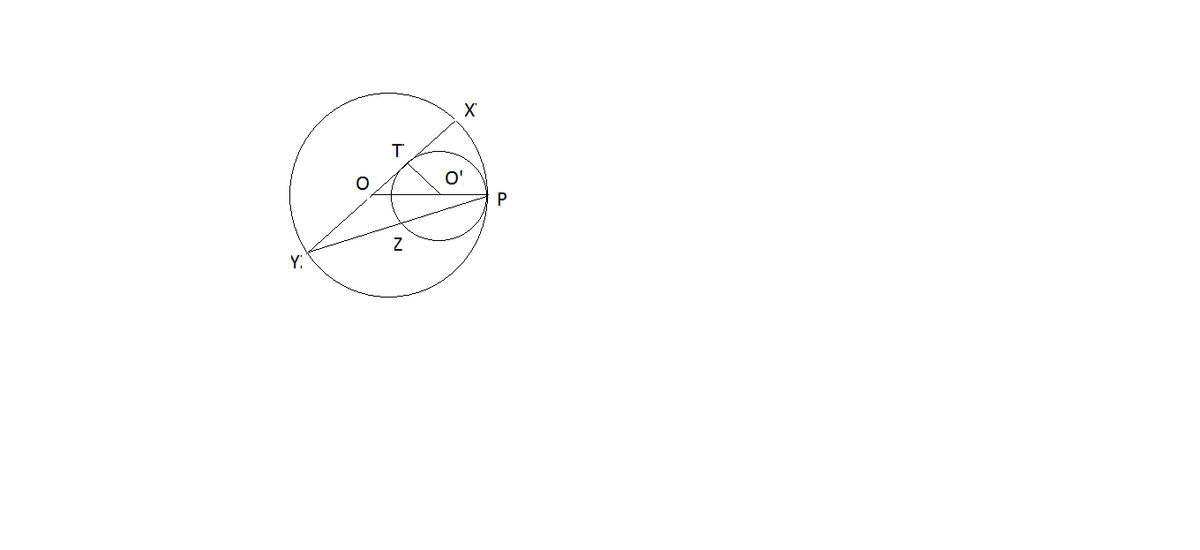
Let O' be the center of smaller circle and the point of tangency is T
Join O' and Z, let <POY=2x
since, OY=OP,we have <OPY=(180-2x)/2=90-x
again,O'Z=O'P we have <OO'Z=2<O'PZ=2(90-x)=180-2x
so,YOO'+ZO'O=180,
Uclid's 5th axiom states OY is parallel to O'Z
now ,watch triangle(YPO') and triangle(ZPO') are similar,
so,O'P/O'O=1/2=O'T/OO'=sin(<O'OT)=30 we are done with,<XYP=1/2(<POX)=15