Circles!!!
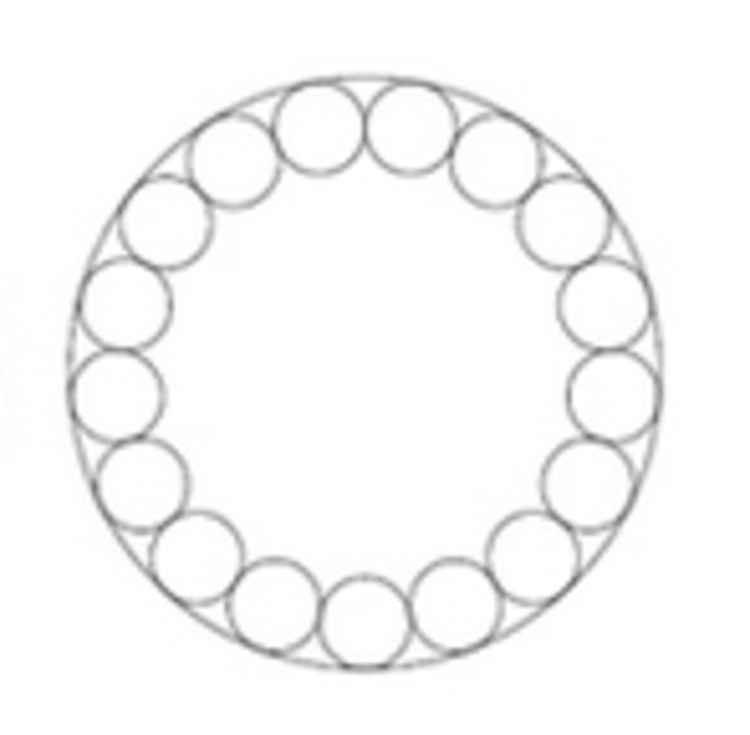 There is a large circle with radius
R
=
4
and
1
7
little circles each having radius
r
, are placed inside on the border of the large circle as shown in the figure.
There is a large circle with radius
R
=
4
and
1
7
little circles each having radius
r
, are placed inside on the border of the large circle as shown in the figure.
Find the value of r .
NOTE : Answer should be rounded to three decimal places.
The answer is 0.6209.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
You can compare the formulas for the area of heptadecagons. This way one doesn’t assume the diameters of the little circles are straight. Hence, minimizing the error from the assumption that the equal legs of the isosceles triangle are (R-r) when this equal legs are actually (R-r+w) where w is a relatively small value in this problem.
Area of heptadecagon = 4 ⋅ tan 1 7 π 1 7 ⋅ s 2 = 2 1 7 ⋅ A ⋅ s
, where A = apothem and s = side length
Since the circle and the imaginary heptadecagon are concentric, we can say that,
A = R-r
And by connecting the little diameters, we can say
s = 2r
Subtituing the expressions, we get :
.
Area of heptadecagon = 4 ⋅ tan 1 7 π 1 7 ⋅ 4 r 2 = 2 1 7 ⋅ ( R − r ) ⋅ 2 r
.
With some algebra we can find "r"... at this point, we can input R = 4
.
Area of heptadecagon = 4 ⋅ tan 1 7 π 2 r = 2 4 − r
r = 1 + cot 1 7 π 4
, then r is around 0.62997 which rounded to 3 decimals is 0.630
This solution is just way longer and based on the fact or assumption (maybe?) that the apothem of the heptadecagon is (R-r), so maybe I can optimize a little bit the solution using the isosceles triangle exposed in your answer, Thanks.
All the centers of the small circles lie on another circle which has a radius of (R-r). As the diameters are quite small, we can assume them as straight lines and thus we get an equation, 2π(R-r) =17×2×r Now, putting the value of R and evaluating the equation, we get value of r=0.621 up to three decimal places.
The centers of two adjoin small circles and the big make an isosceles triangle with sides (R-r),( R-r) and 2r, the angle between (R-r),( R-r) being, 1 7 3 6 0 . R − r r = S i n 1 7 1 8 0 . ∴ s o l v i n g f o r r , R = 4 , w e g e t r = . 6 2 0 9 .