Circles
x 2 + y 2 + 3 2 ( x + y ) = 0 x 2 + y 2 + 5 2 ( x + y ) = 0
Consider the equations of the two circles above. A third circle is drawn internally tangent to the larger circle, externally tangent to the smaller circle, and tangent to their common diameter. If the third circle's radius can be written as p 2 p − 1 , then what is the value of p ?
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Relevant Wiki: Descartes' Circle Theorem
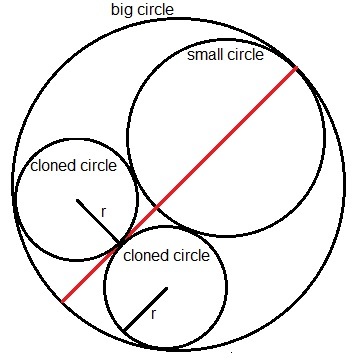
By some calculation, we will know that two known circles' radius are 3 and 5,
because the wanted circle is tangent to the red line, so it is sufficient to clone the circle, as the figure above. It will do a great help. (Also sorry for the figure, it should has only one cloned circle.)
let k 1 = 3 1 , k 2 = − 5 1 , k 3 = k 4 = r 1 , the sign of k's are respect to if it where externally tangent or internally tangent to each other.
2 ( k 1 2 + k 2 2 + k 3 2 + k 4 2 ) = ( k 1 + k 2 + k 3 + k 4 ) 2
2 ( 9 1 + 2 5 1 + r 2 2 ) = ( 3 1 − 5 1 + r 2 ) 2
Solving this, yield r = 8 1 5 .
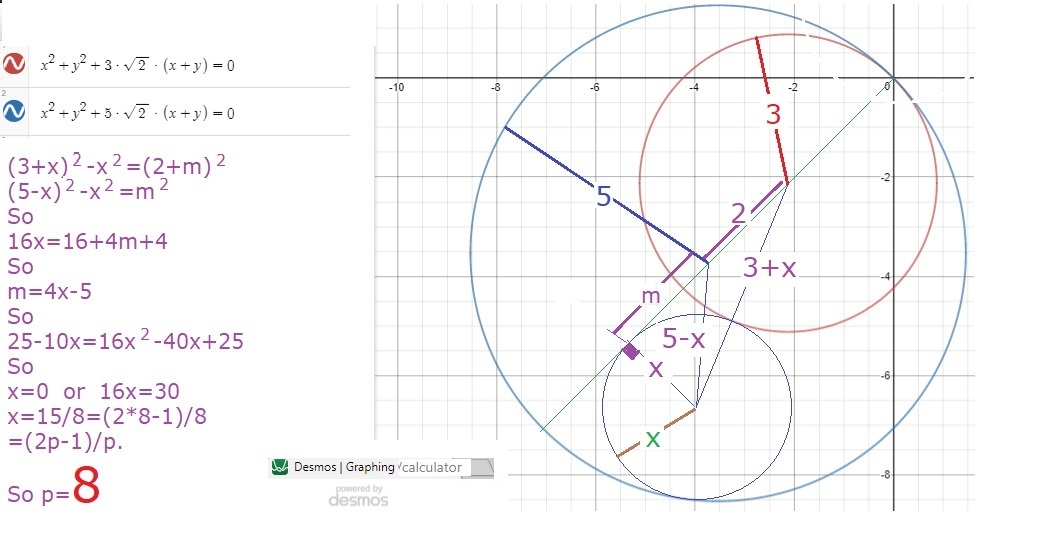
( r + 3 ) 2 − r 2 = 2 + ( 5 − r ) 2 − r 2
9 + 6 r = 2 + 2 5 − 1 0 r
4 r − 3 = 9 + 6 r
1 6 r 2 − 2 4 r + 9 = 9 + 6 r , r = 8 1 5
Hence
p = 8
And radius of circle can be known by rearrange form of equation that was given.