Circles!

I really like this problem, and here is my solution. It is most likely not going to be the solution that you find.

Invert about the point $P$ , using a circle $\mathfrak{C}$ whose radius is equal to the diameter of the congruent circles. The point $P$ goes to the point at infinity. Hence, all of these circles transform into lines. These lines will be tangential to the circle $\mathfrak{C}$ .

As an example, I have drawn 3 circles (blue, red, green) that pass through a common point P. We invert with respect to the black circle, to obtain the corresponding colored lines.

Since no set of 3 congruent circles can pass through the same 2 points, we know that no 3 lines (after inversion) are concurrent. Hence, if no 2 (inverted) lines are parallel, we will have ${ 1000 \choose 2 } + { 1000 \choose 1 } + { 1000 \choose 0 }$ regions.

Inverting back, we see that this is the same number of regions that the circles are cut into.

Corollary: If every pair of circles intersect in their interior, then the number of regions is 500501.

consider the common point to be a line segment the circles can then be considered triangles of equal height (as Calvin sir pointed out below this is because the circles have equal radii) on the line segment.(this is sort of like using mercator's projection).
then drawing we can easily see that no of regions for n circles.
( $\sum_{i=1}^n$ i ) +1=n(n+1)/2+1 .
the image below for n=5 should make my point clearer.

putting n=1000 we have the answer as 1000(1001)/2+1.
=500501

Let the number of regions formed by $n$ circles be $F(n)$ for all natural numbers $n$ .

If there're $n+1$ circles, there are $F(n+1)$ regions.

We will count another way.

For each $(n+1)^{th}$ circle created, the $(n+1)^{th}$ circle will create more regions on $n$ circles. which has $F(n)$ regions, by creating on each $n$ inside regions and $1$ outside region, total $F(n)+(n+1)$ regions. We'll list all the cases that regions aren't maximized and all the solutions.

• If 2 centers, and point $P$ are collinear, the 2 circles will not intersect at 2 points, which doesn't maximize the number of regions. Therefore, no 2 sets of points are collinear with point $P$ .
• If 3 circles are set as figure 1 below, we see that circle $C$ doesn't create a region on region $A \cap B$ if point $C$ are between ray $\overrightarrow{AO}$ and $\overrightarrow{BO}$ . This can be solved by not making this happen. One of my suggestions is to condense every circles on either side of the line (colored red) by figure 2 below.

Figure 1

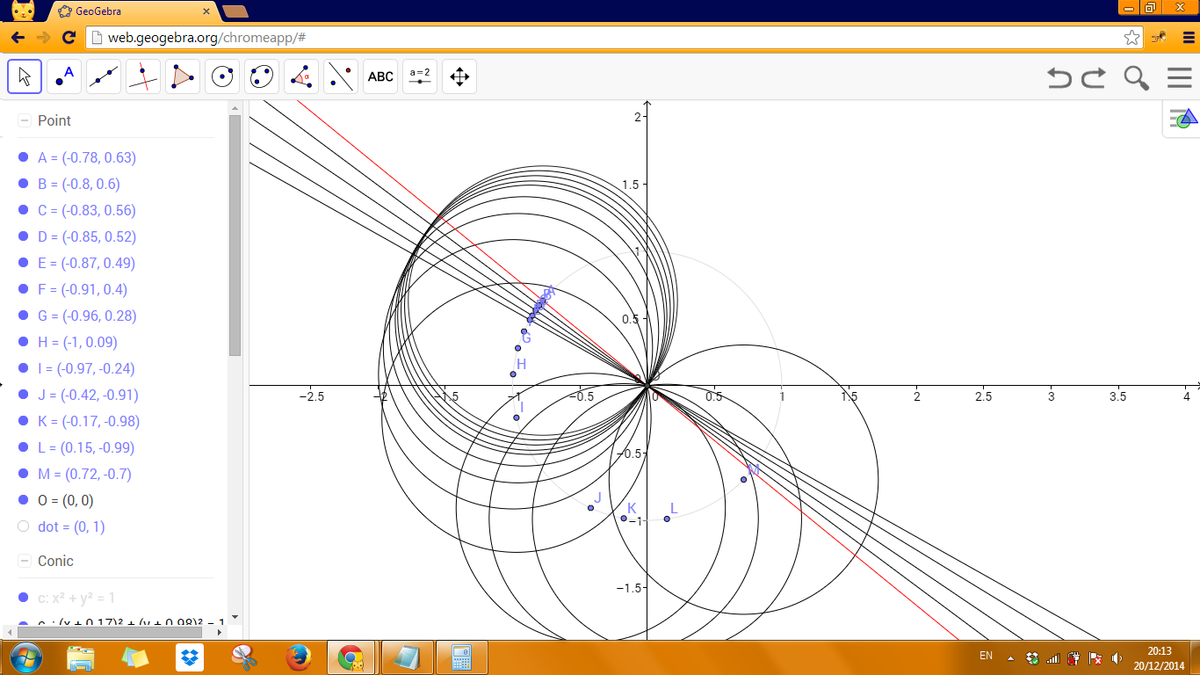Figure 2

The number of regions of $n+1$ circles is $F(n+1)$ regions, and we counted another way we get $F(n)+(n+1)$ regions.

Therefore, $F(n+1) = F(n)+(n+1)$ .

Which means $F(n)$ is a triangular number and a constant!

i.e. $\displaystyle F(n) = \frac{n(n+1)}{2}+c$ .

Since $F(1) = 2$ , we get $c = 1$ .

Therefore, $\displaystyle F(n) = \frac{n(n+1)}{2}+1$ .

Plug in $n = 1000$ we get $F(1000) = \boxed{500501}$ . ~~~

When you draw first circle on a plane, it divides the it in 2 regions. Then second circle divides it in 4 regions, the third in 7, fourth in 11, fifth in 16 and so on.. So it forms a second order Arithmetic Progression : 2,4,7,11,16,22,.... Whose 1000th term will be the required answer.

The primary Arithmetic Progression in this is 2,3,4,5,6,...., 999. Find sum of this = 500499 and add the first term of the second orde progression to get 500501.

P.S. : looks like a very crude way of solving but it worked! I'd love if someone adds more explaination to it..

When we draw the first circle, we form 1 region and cross 0 existing circles. When we draw the second circle, we form 1 more region and cross 1 existing circle. While crossing this existing circle, we divide it into 2 regions region. When we draw the third circle, we form 1 more region and cross 2 existing circles. When we cross those 2 existing circles, we divide them in once more and create 2 new regions.

From this, it becomes clear that every time we cross an existing circle, we make a new region and drawing the circle itself creates a new region. (If you draw it out, you'll see immediately) This means that when we draw the nth circle, we make 1 region and cross n-1 existing circles to make a total of n regions.

Now sum from 1 to 1000 and add 1 for the region outside the circles to get 500501. Note that none of the circles can be drawn at a 180 degree angle to another circle because that means that the circle did not cross the circle 180 degrees from it. For example, the red circle and the teal circle in the picture from the problem never cross and form 2 regions instead of 3.

Let $n$ be number of circles

$U_n=\dfrac12n^2+\dfrac12n+1$

1000 circles

$U_{1000}=\dfrac12(1000)^2+\dfrac12(1000)+1=500501$