Circles
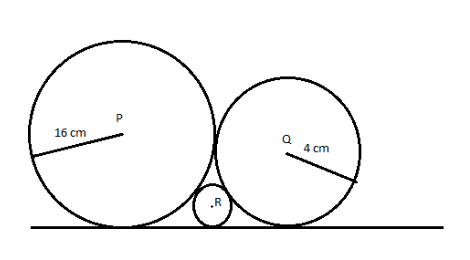 Three circles with centers P, Q and R touch each other externally.
Three circles with centers P, Q and R touch each other externally.
One of their common tangents is touching as shown in the figure.
Find the radius of the circle with center R.
(Correct to two decimal points)
The answer is 1.77.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
A specialized case of Descartes' Theorem for three tangential circles and a line is k 4 = k 1 + k 2 + 2 k 1 k 2 , where k 1 = r 1 1 , k 2 = r 2 1 , and k 4 = r 4 1 . In this problem, k 1 = 1 6 1 , k 2 = 4 1 , and k 4 = R 1 . Substituting, we get R 1 = 1 6 1 + 4 1 + 2 1 6 1 4 1 , and solving we get R = 9 1 6 ≈ 1 . 7 7
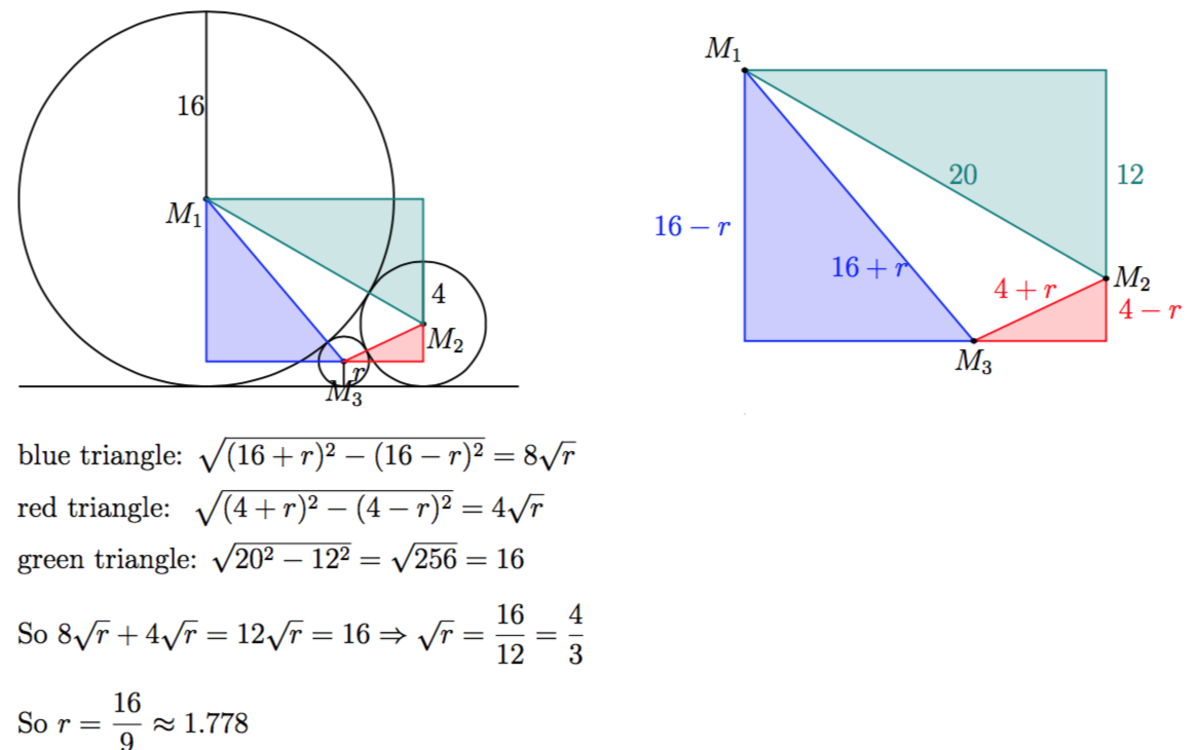
to solve sums like this ... i.e., involving a common tangent ...... there is a formula which can b applied for this case
"1/root(R) = 1/root(R1) + 1/root(R2)"
where R = Radius of small circle; R1 and R2 are the radii of the other two circles
Applying the formula, v get Reqd. radius = 1.77 / 1.78
i wud post the proof of the formula within a few days ...