Circles!
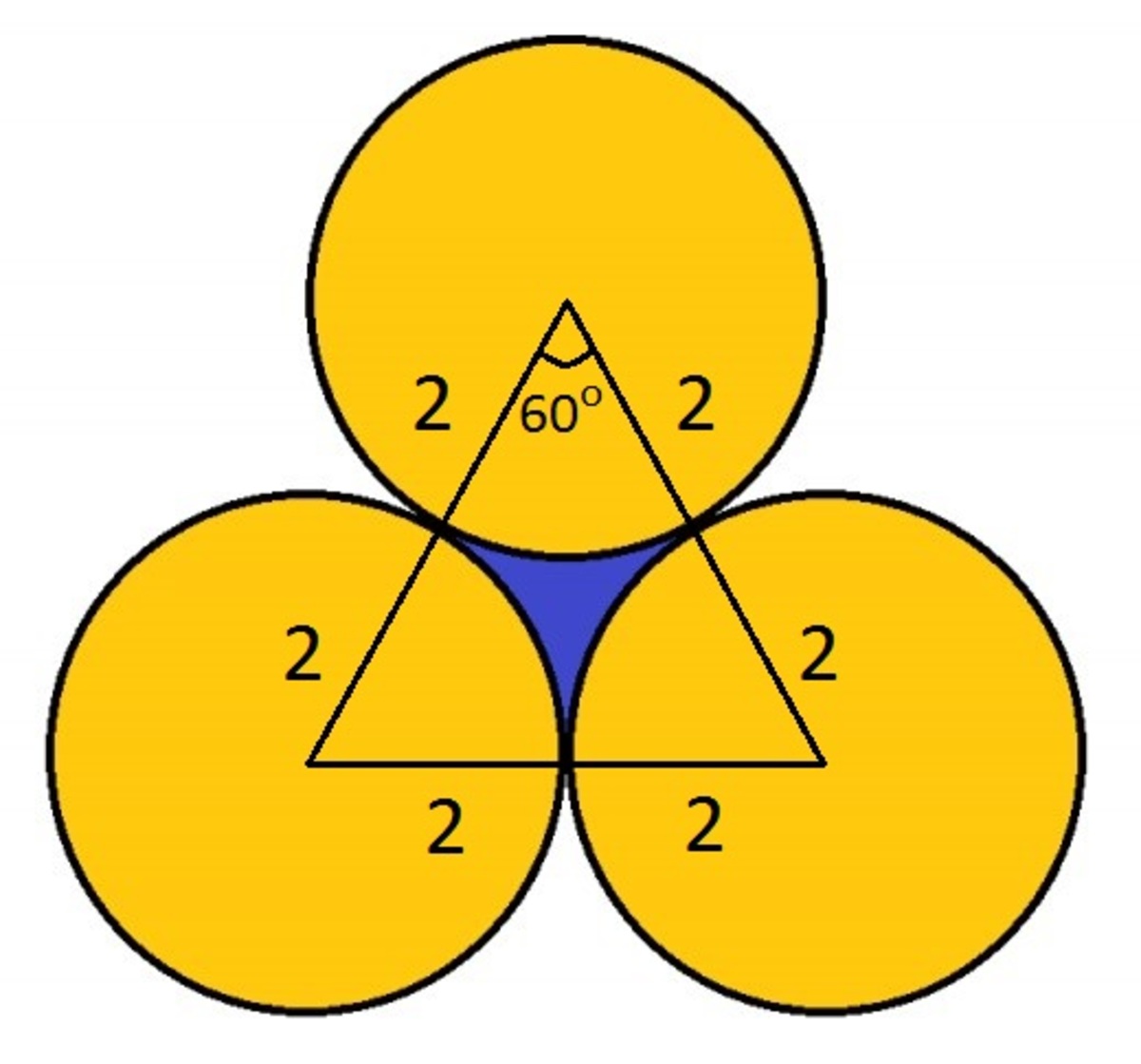
 Three circles, each with a radius of 2, are mutually tangent. What is the area of the region bounded by the three circles, shown in blue above?(Answer correct to 4 decimal places).
Three circles, each with a radius of 2, are mutually tangent. What is the area of the region bounded by the three circles, shown in blue above?(Answer correct to 4 decimal places).
The answer is 0.6450.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Discussions for this problem are now closed
Let r = Radius = 2 , t = Area of triangle , c = Area of circle sector and a = Area
Join the centre of each circle to the other circles centres to form an equilateral triangle with a side length of 2 r
Next you work out the area of said triangle using the following formula
t = 2 b ⋅ h
Since you don't know the height ( h ) of the triangle, we need to find it. To do this we split the triangle into two equal right-angled triangles with a base ( b ) and a side length of 2 r .
Since we split it in half we can say that
b = r
Now that we have a right-angled triangle we can use Pythagorean theorem ( a 2 + b 2 = c 2 )
We only know a and c so we can just insert them into the formula
( r ) 2 + b 2 = ( 2 r ) 2 ∴ b = r 3
So now we can return to the original triangle and work out it's area.
b = 2 r , h = r 3
t = 2 2 r ⋅ r 3 = r 2 3
t = r 2 3
Now we need the area of the sectors (part of a circle) inside the triangle
To do that we need this formula
c = 2 θ r 2
This however only works when we have the angle in radians. So what is the angle?
When the centres were joined they created and equilateral triangle, all of it's angles are 6 0 ∘ . So
θ ∘ = 6 0 ∘
But we need θ in radians
6 0 = 6 1 ⋅ 3 6 0 = 6 1 ⋅ 2 π = 3 π
So θ = 3 π
Now onto the formula
c = 2 ( 3 π ⋅ r 2 ) = 6 π r 2
c = 6 π r 2
To find the shaded area we need to take the area of the three circle sectors from the area of the triangle so
a = t − 3 c
The values can be substituted in
a = r 2 3 − 3 ( 6 π r 2 )
This goes to
a = 2 2 r 2 3 − π r 2
Since r = 2 we can put that in to get an answer
a = 2 2 ( 2 ) 2 3 − π ( 2 ) 2 = 2 8 3 − 4 π
This simplifies down to
a = 4 3 − 2 π = 0 . 6 4 5 0 1 7 9 2 3 0 9 5 8 8 …
Since the problem only asked for the answer to 4.d.p we can say the answer is 0 . 6 4 5 0
3 circles of same radius are mutually tangent implies the line joining their centres form an equilateral triangle.
Area of blue = Area of equilateral triangle - 3 * area of sector = root 3 * 16 /4 - 3* (60/360) pi 4 = 0.645 sq.units
Let us consider the radius as r
If we join the 3 centers of each, we get an equilateral triangle with side 2 + 2 = 4
Using Heron's formula, where S=6 , a=4 b=4 c=4 , the area of the triangle approximates to 6.93 square units
Now, consider the sectors of each circle. Since its an equilateral triangle, each angle will be 60 degrees. There are 3 such sectors.
Area of all 3 sectors = 3 × ( 6 0 / 3 6 0 ) × p i × r 2
Simplifying, and substituting value of 'r', We get, area is approximately 6.285 units.
6.93 - 6.285 = 0.645
Imagine the centres of the three circles to form an equilateral triangle with a side length of 2r., which is 4. The area of the triangle can be calculated using Heron's Formula, which is:
A = {s(s-a)(s-b)(s-c)}^(1/2), where s is the semiperimeter of the triangle; that is, s={a+b+c}/2. In this case, s=6, A=[6(2)(2)(2)]^(1/2)=6.9282.
Notice that the area of the triangle consist of the area of the region bounded by the three circles(the blue area) and three equal circular sector.
The formula for the area circular sector: A=θ(pi)(r^2)/360, where θ is the angle of between the two radii. Since the triangle is equilateral, θ=60, hence the area of the three sectors=3(60)(pi)(4)/360=6.2832
Hence, the area of the region bounded by the three circles(blue area)= 6.9282-6.2832=0.645.
Because the 3 circles are mutually tangent, we can draw a triangle from the centers of the circles. We can easily find the area of this triangle, and the areas of the 3 sectors, then we will find the area of the blue region.
This triangle is an equilateral triangle, because it has 3 equal sides each of which is 4.
Area of triangle = (√3)/4 × 4^2 = 4√3
Area of a sector = (πr^2 × 60)/360 = (πr^2)/6 = (π × 2^2)/6 = (π × 4)/6 = 2π/3
=> Area of 3 sectors = 2π/3 × 3 = 2π
Therefore, the area of the blue region = 4√3-2π = 0.645
Answer: 0.645