Circles and a Square
A small circle with radius 3 is enclosed by square which is also enclosed by a bigger circle.
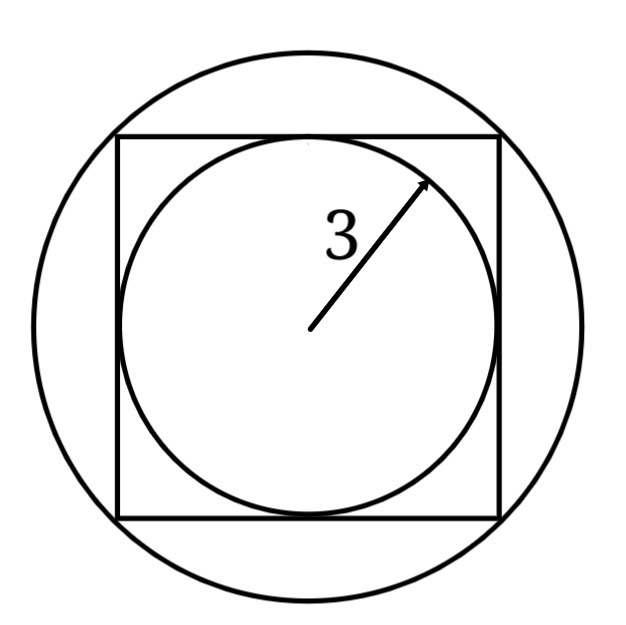
The ratio between the bigger circle and the smaller circle's circumference can be expressed as . What is the value of ?
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The side length of the square which is also the diameter of the small circle is twice the radius of the small circle and it is 2 × 3 = 6 . The diameter of the big circle which is also the diagonal of the square can be found by using the pythagorean theorem and it is 6 2 . Now that we know the diameter of the small and the big circle, we need to find their circumferences. The circumference of a circle is given by c = π d where d is the diameter of the circle. By using the formula, the circumference of the small circle is 6 π and the big circle is 6 π 2 . To find the ratio of the circumference of the bog circle to the circumference of the small circle, we need to divide
r a t i o = c i r c u m f e r e n c e o f t h e s m a l l c i r c l e c i r c u m f e r e n c e o f t h e b i g c i r c l e = 6 π 6 π 2 = 2
It is of the form n as required in the problem. The required answer is 2 .