Circles and a... Triangle
A small circle is drawn such that its circumference is touching the edges of an equilateral triangle. A bigger circle is draw such that the circumference is touching the vertices of the equilateral triangle.
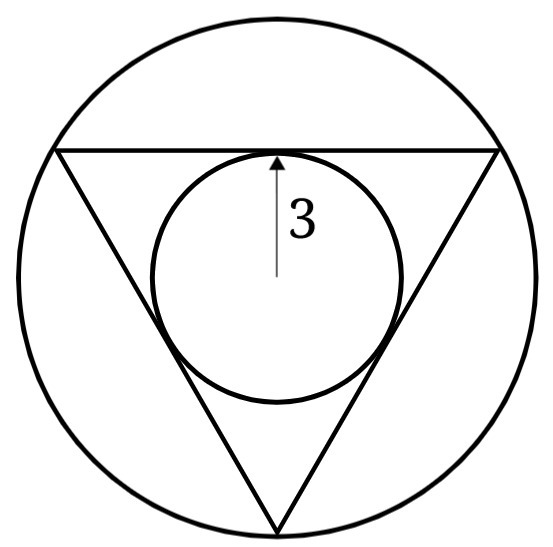
The ratio between the bigger circle and smaller circle's circumference can be written as c s c ( θ ) .
S m a l l C i r c l e ′ s C i r c u m f e r e n c e B i g C i r c l e ′ s C i r c u m f e r e n c e = c s c ( θ )
What is the value of θ if 0 ∘ < θ < 9 0 ∘ .
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Simple, just join the center of the small circle to the vertex of the equilateral triangle.
It becomes a right angled triangle.
The angle formed at the vertex is 3 0 ∘
Using basic Trigonometry, we have sin 3 0 ∘ = x 3 , where x is the radius of the bigger circle as well as the hypotenuse.
∴ x = 6
Now, we know both the circles' radii, i.e. 3 and 6 .
Required ratio = c o s e c θ = 2 π ( 3 ) 2 π ( 6 ) = 3 6 = 2
⟹ θ = 3 0 ∘
If we draw a line from the centers of the circles to the top left vertex of the triangle, we have a right triangle as in the diagram to the right. Because 2 of this triangle's sides are the radii of the circles, we can use a trigonometric function to describe their ratio.
If we use the angle labeled θ in the diagram, the ratio of the big circle's radius to the small circle's radius turns out to be csc ( θ ) , as the problem asks for. Now all we have to find is the value of θ . Because this triangle is equilateral, each angle is 6 0 ∘ , and because θ is half of this, our final answer will be 3 0 ∘