Inscribed Isosceles Triangle
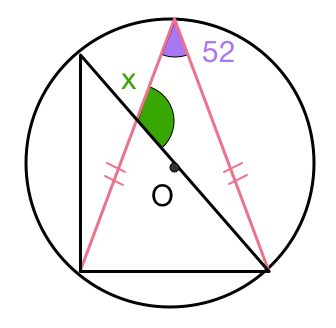
Find the value of . The two indicated sides are congruent. is the center of the circle.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
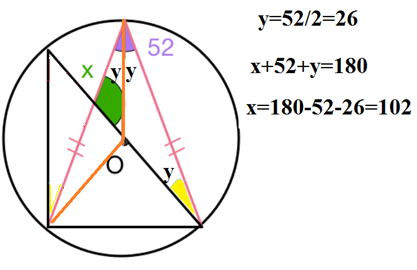
Method 1 : Apply Thales Theorem .
Let's denote the points A , B , C , D and E as shown below.
Because A O C is a straight line that passes through the center O , then the triangle C B A is a right triangle with ∠ C B A = 9 0 ∘ by Thales' Theorem.
And note that the triangle B D A is an isosceles triangle with B D = A D , so ∠ D B A = ∠ D A B = 2 1 8 0 ∘ − 5 2 ∘ = 6 4 ∘ .
Thus ∠ C B E = ∠ C B A − ∠ D B A = 9 0 ∘ − 6 4 ∘ = 2 6 ∘ .
Apply the properties of Inscribed Angle Theorem , we have ∠ B C A = ∠ B D A = 5 2 ∘ .
Because ∠ C E B = ∠ D E A = x ∘ , and we know the sum of angles of a triangle is 1 8 0 ∘ , so
∠ C B E + ∠ B E C + ∠ E C B 2 6 ∘ + x ∘ + 5 2 ∘ x ∘ x ∘ x = = = = = 1 8 0 ∘ 1 8 0 ∘ 1 8 0 ∘ − 2 6 ∘ − 5 2 ∘ 1 0 2 ∘ 1 0 2
Method 2 : Apply Inscribed Angle Theorem only.
Let's denote the points A , B , C , D and E as shown below.
By inscribed angle theorem, ∠ B O A = 2 ∠ B D A = 2 ( 5 2 ∘ ) = 1 0 4 ∘ .
Because B O = O A represents the radius of the circle, then the triangle B O A is an iscosceles triangle with ∠ O B A = ∠ B A O = 2 1 8 0 ∘ − 1 0 4 ∘ = 3 8 ∘ .
Similarly, because B D = A d , then the triangle B D A is an isosceles triangle with ∠ B A D = ∠ D B A = 2 1 8 0 ∘ − 5 2 ∘ = 6 4 ∘ .
And so, ∠ D A E = ∠ D A B − ∠ O A B = 6 4 ∘ − 3 8 ∘ = 2 6 ∘ .
By referring to triangle D E A , we have
∠ D E A + ∠ E A D + ∠ A D E x ∘ + 2 6 ∘ + 5 2 ∘ x ∘ x ∘ x = = = = = 1 8 0 ∘ 1 8 0 ∘ 1 8 0 ∘ − 2 6 ∘ − 5 2 ∘ 1 0 2 ∘ 1 0 2