Circles And Circles And Circles
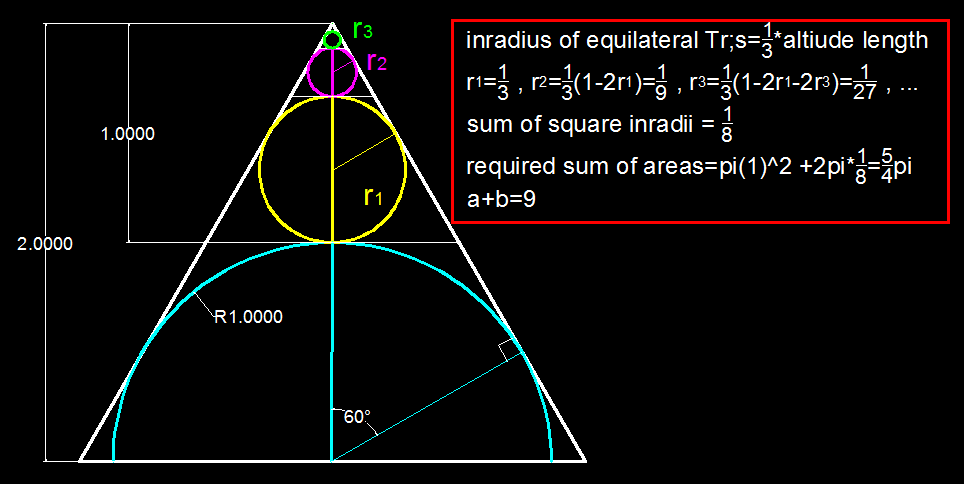
Two equilateral triangles are joined to create a rhombus. A circle is inscribed so that its center lies on the midpoint of the triangle sides that touch. Two more circles are inscribed, one on each side of the largest circle, such that they touch the sides of the triangle and the largest circle. This pattern repeats to infinity as shown.
Given that the radius of the largest circle is 1, find the sum of all circle areas, that is, the sum of the blue shaded region.
If the area can be expressed as , where and are coprime positive integers , input as your answer.
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let us just focus on the right side of the symmetrical figure. The figure above shows part of the largest circle and the next two largest circles with centers at A , B and C respectively. Since the triangle is equilateral, then all its interior angles are equal to 3 1 8 0 ∘ = 6 0 ∘ , so ∠ A G D = 2 6 0 ∘ = 3 0 ∘ and so ∠ G A D = 1 8 0 ∘ − 9 0 ∘ − 3 0 ∘ = 6 0 ∘ .
Thus, cos ∠ G A D = A D A G ⇒ cos 6 0 ∘ = 1 A G ⇒ A G = 2 .
Let r 1 > r 2 > r 3 > ⋯ be all the radii of the subsequent circles. So in the figure, we see that r 1 = B E and r 2 = C F .
Then B G = A G − A B = 2 − 1 − r 1 = 1 − r 1 . Because △ A D G ∼ △ B E G , then A B A G = B E B G ⇒ 1 2 = r 1 1 − r 1 ⇒ r 1 = 3 1 .
Likewise, C G = A G − A B − B C = 2 − ( 1 + r 1 ) + ( r 1 + r 2 ) = 1 − 2 r 1 − r 2 and because △ A D G ∼ △ C F G , then
A B A G = B E B G ⇒ 1 2 = r 2 1 − 2 r 1 − r 2 ⇒ r 2 = 9 1 .
If we continue on this pattern, we see that r 3 = 2 7 1 , r 4 = 8 1 1 , r 5 = 2 4 3 1 . This suggests that r n = 3 n 1 .
By looking at the working above, it's not hard to extract out the recursive formula, 3 r n = 1 − 2 k = 1 ∑ n − 1 r k , where k = 1 , 2 , 3 , … . A simple induction shows that r n = 3 n 1 is indeed true.
Hence, the area in the right figure is equal to the sum of area of the semicircles and the areas of the circles with radii r 1 , r 2 , … . That is,
Area in the right figure = = = = 2 1 π R 2 + π r 1 2 + π r 2 2 + π r 3 2 + ⋯ 2 1 π + π k = 1 ∑ ∞ r k 2 2 1 π + π k = 1 ∑ ∞ 9 k 1 2 1 π + π ⋅ 1 − 1 / 9 1 / 9 = 8 5 π ,
With the series in the penultimate step follows a geometric progression sum .
Doubling this number gives the desired area 4 5 π , and so a + b = 5 + 4 = 9 .