Circles and Parabolas
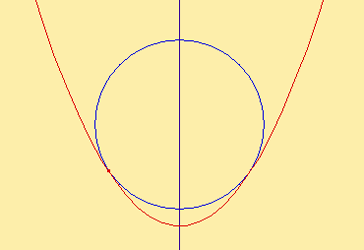 Compute the radius of the circle that is inscribed between the x‐axis and the equation
Compute the radius of the circle that is inscribed between the x‐axis and the equation
y = 5 0 0 x ( x − 2 0 1 4 )
The answer is 757.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice solution. I didn't go with the change of variables. I just wrote the circle equation as (x - 1007)^2 + (y + r)^2 = r^2, expanded to get
x(x - 2014) + 1007^2 + y^2 + 2ry = 0,
and then swapped x(x - 2014) with 500y to find the points of intersection with the parabola. This gives us the quadratic in y
y^2 + (500 + 2r)y + 1007^2 = 0.
Now by symmetry the two points of intersection have the same y-value, so the discriminant must be 0, yielding that 250 + r = 1007, and so r = 757
The equation of the circle would be
( x − 1 0 0 7 ) 2 + ( y + r ) 2 = r 2
Where r is the radius of the circle.
Expressing r in terms of y ( x − 1 0 0 7 ) 2 + ( y + r ) 2 = r 2 5 0 0 x ( x − 2 0 1 4 )
would give r = 2 y − ( y 2 + 5 0 0 y + 1 0 0 7 2 )
Since the circle is tangent with the parabola, it means that they would only "intersect" at 2 points and not 4 points. Furthermore, the y value has to be negative. This means that we have to find the minimum of r for only 2 intersections to occur with the conditions that y is negative. This comes out as y = 1 0 0 7 and r = 7 5 7
We will consider a change of variables and let our parabola be y = a ( x − d ) ( x + d ) .
The circle to be inscribed within this parabola and the x-axis is x 2 + ( y + r ) 2 = r 2 .
Substituting the first equation into the second yields a quadratic in x 2 . In order to have the circle tangent to the parabola we need to have exactly two solutions to the system of equations. We can satisfy that condition by setting the discriminant of our quadratic to zero. This yields
4 a 2 r 2 + 4 a r + 1 − 4 a 2 d 2 = 0 .
Solving for r and taking the positive root we find that r = 2 1 ( 2 d − a 1 ) . For the original problem the solution would be 7 5 7 .
One should note that if we set 2 r = ∣ y ( 0 ) ∣ = a d 2 we see that a d = 1 . This is the limiting case. In other words, if we have a d = 2 1 a Δ x i ≤ 1 , then the curvature of the parabola at the vertex is lower than the circle with diameter from the vertex to the x-axis, and the radius in this case would just be 2 1 ∣ y ( 0 ) ∣ . This is not the case in our original problem, so this possibility need not be considered.
Again looking at the original problem we can relate this to the general case of a parabola of the form y = a x 2 + b x + c and say that the radius of the circle inscribed between the parabola and the x-axis is r = 2 1 ( Δ x i − ∣ a 1 ∣ ) , or 2 1 ∣ y ( 2 a − b ) ∣ , if a > Δ x i 2 , where Δ x i equals the discriminant b 2 − 4 a c , or the difference between the real roots of the parabola.