Circles and Squares
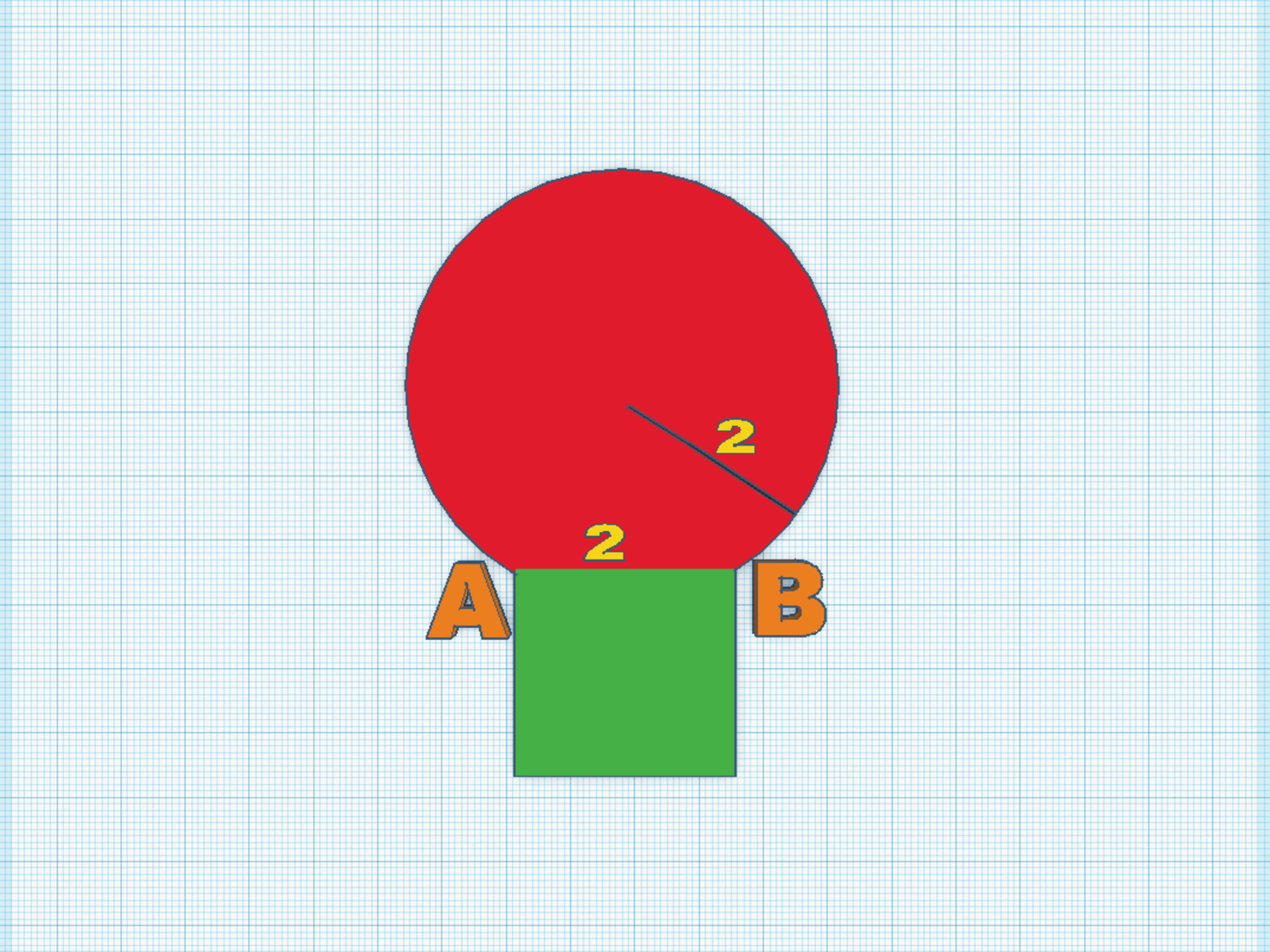 A circle with a radius of 2 has a chord
A
B
of 2. A square with a side
A
B
is constructed, leaving the two other vertices outside the circle. If the total area of the figure can be expressed as
b
a
π
+
c
+
d
, where a and b are relatively prime, what is
a
+
b
+
c
+
d
?
A circle with a radius of 2 has a chord
A
B
of 2. A square with a side
A
B
is constructed, leaving the two other vertices outside the circle. If the total area of the figure can be expressed as
b
a
π
+
c
+
d
, where a and b are relatively prime, what is
a
+
b
+
c
+
d
?
Note: A is not equal to a , and B is not equal to b
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I think you have a typo there. It should say +square not -square. But it is a good problem. Thanks.
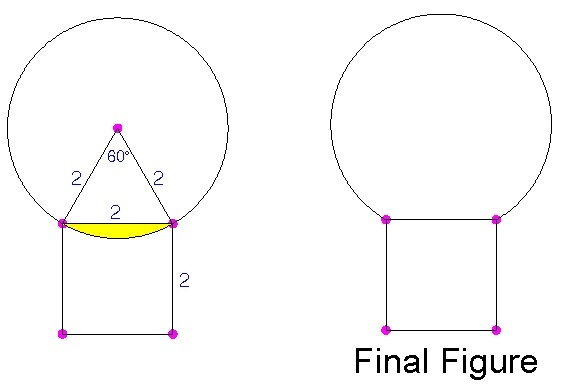
A s e c t o r = 3 6 0 6 0 π r 2 = 3 6 0 6 0 π ( 2 2 ) = 3 2 π
A t r i a n g l e = 4 s 2 3 = 4 2 2 3 = 3
A s e g m e n t = A s e c t o r − A t r i a n g l e = 3 2 π − 3
let A be the total area of the figure
A = Area of the square + Area of the circle - Area of the segment
A = 2 2 + π ( 2 2 ) − ( 3 2 π − 3 ) = 3 1 0 π + 3 + 4
Finally,
a + b + c + d = 1 0 + 3 + 3 + 4 = 2 0
You could draw an equilateral triangle by connecting A and B to the center point. That makes an equilateral triangle with a side of 2, so the area of the overlapping part is 3 2 π − 3 . The area of the circle is 4 π , and the area of the square is 4 . The area of the whole figure is area of the circle - overlapping part + square which is equal to 4 π − ( 3 2 π − 3 ) + 4 which is 3 1 0 π + 3 + 4 . Therefore, a + b + c + d = 1 0 + 3 + 3 + 4 = 2 0