Circles Can be Cool Too!

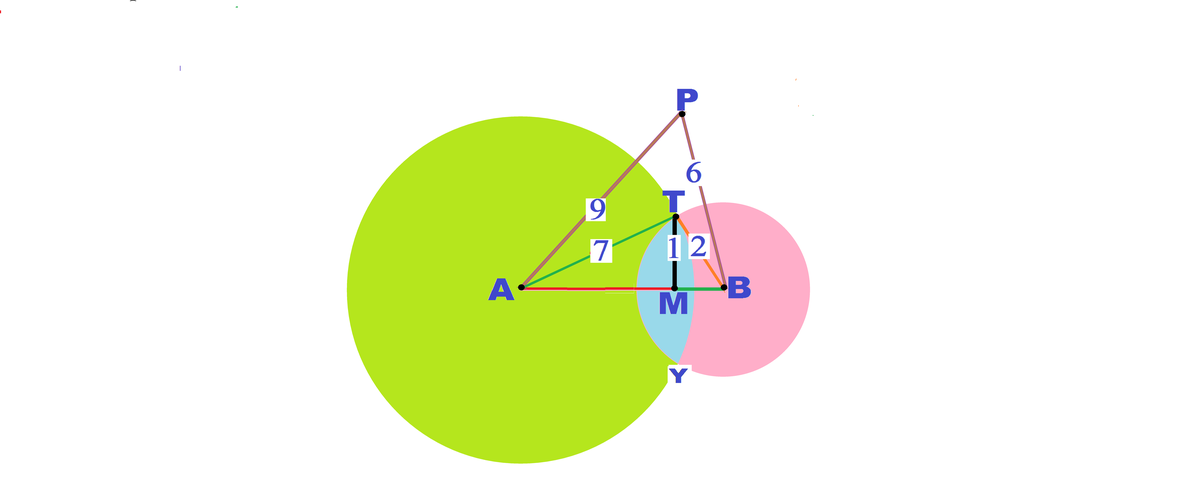Let's call the points where line PA intersects circle $\omega _ 1$ $X_1$ and $X_2$ . Likewise, let's denote the points where line PB intersects circle $\omega _2$ as $Y_1$ and $Y_2$ . First notice that since the radius of the first circle is 7, $PX_{1}=2$ and likewise, since the radius of the second circle is 2, $PY_{1} = 4$ . Notice that the power of P with respect to both circles are equal ( $2 \times 16 = 4 \times 8$ ), therefore, P lies on the radical axis of both of these circles. This implies that if you drop a perpendicular down from P to AB, the segment will pass through T and Y and will be the height of $\bigtriangleup PAB$ . Call the foot of the perpendicular C.

Now, our overall goal is to find the lengths of AC and BC because then we can just use the triangle area formula to finish. Luckily this is pretty easy! Just connect A with T and notice the AB is the perpendicular bisector of TY, therefore $TC = \frac{2}{2} = 1$ . Now use the Pythagorean Theorem to find that $AC = 4\sqrt{3}$ . Likewise, you find that $BC = \sqrt{3}$ .

We have the bases! Now we just need to find PC, the height! Luckily this is also very easy because we can use the Pythagorean Theorem on either PAC and PBC to get that $PC = \sqrt{33}$ (Don't worry, I checked on both triangles). Now, the total area of $\bigtriangleup PAB$ is just $\frac{\sqrt{33}}{2}(4\sqrt{3}+\sqrt{3}) = \frac{15\sqrt{11}}{2} \implies a+b+c = 15 + 11 + 2 = \boxed{28}$ .

The distance between A and B can be found using the property that perpendicular dropped from centre to chord of circle bisects chord and the Pythagoras theorem for each of the two circles. Once we have AB area can be easily found using Heron's Formula.

$Let ~ M ~ be ~ the ~ midpoint ~of ~TY.\\ \text{ Since common chord and line of centers intersect at M,}\\ \text{In rt, angled triangles APM and BPM, }\\ AM=\sqrt{AP^2 - PM^2}=\sqrt{48}=4\sqrt3, ~ and ~ BM=\sqrt{BP^2 - PM^2}=\sqrt{3} .\\ In ~ \Delta PAB, ~AB=5\sqrt3, PA=9, ~ PB=6,~ by ~ Hero's~ Formula,~ Area~\Delta PAB=\Large 28$
Sketch not to scale.