Circles in a rectangle - question 1
 In the figure, all circles are tangent to each other, as well as to the sides of the rectangle. The two red circles are congruent and the blue one is a unit circle.
In the figure, all circles are tangent to each other, as well as to the sides of the rectangle. The two red circles are congruent and the blue one is a unit circle.
If the area of the rectangle can be expressed as a + b b , where a and b are integers, find a + b .
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
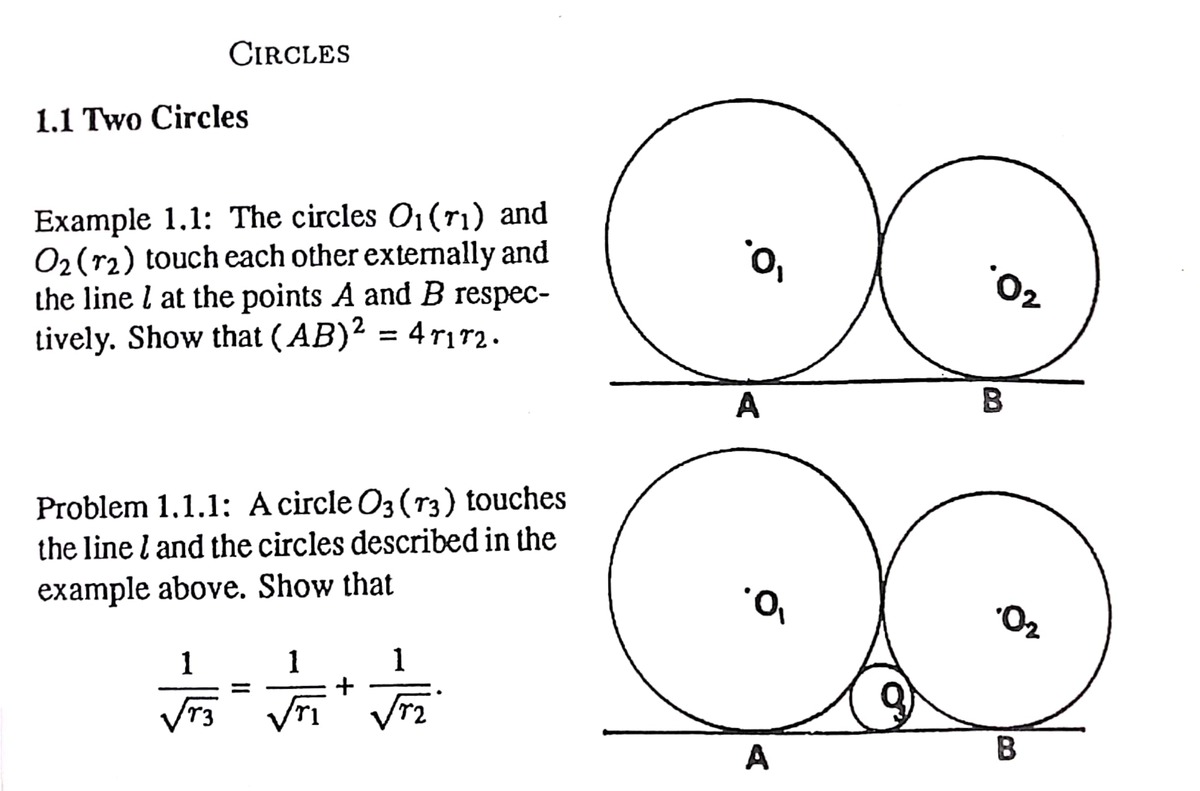
Nice and clear! It is worth mentioning that both the expression for the length of common tangent segment of two circes and the "kissing circles theorem" are two well known sangaku problems. In fact they are the firts two problems in
Fukagawa, Hidetoshi, and Dan Pedhoe. 1989, Japanese temple geometry problems, Winnipeg: Charles Babbage Research Centre
(seen in the picture).
 A slight typo in your solution: instead of "=CD" I guess it is "=CE".
A slight typo in your solution: instead of "=CD" I guess it is "=CE".
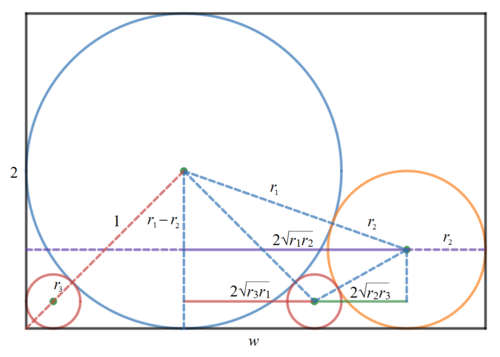
Let the radii of the blue, yellow, and red circles be r 1 , r 2 , and r 3 respectively. Then we note that the length of the purple (full) line is given by ℓ p u r p l e = ( r 1 + r 2 ) 2 − ( r 1 − r 2 ) 2 = 2 r 1 r 2 . Similarly, those of the red and green lines are ℓ r e d = 2 r 3 r 1 and ℓ g r e e n = 2 r 2 r 3 . Since ℓ p u r p l e = ℓ r e d + ℓ g r e e n , we have:
2 r 1 r 2 ⟹ r 2 = 2 r 3 r 1 + 2 r 2 r 3 = r 1 − r 3 r 3 r 1
⟹ r 3 1 = r 1 1 + r 2 1
Given that r 1 = 1 , and we can find r 3 by consider the red circle on the left. We note that the length of the red dash line is 2 = 1 + r 3 + 2 r 3 ⟹ r 3 = 2 + 1 2 − 1 = ( 2 − 1 ) 2 . Therefore r 2 = 1 − 2 + 1 2 − 1 = 2 1 .
Let the width of the rectangle be w . We note that w is the length of the purple dash/full line, which is w = r 1 + 2 r 1 r 2 + r 2 = ( r 1 + r 2 ) 2 = ( 1 + 2 1 ) 2 = 2 3 + 2 2 . The area of the rectangle is 2 w = 3 + 2 2 . Therefore a + b = 3 + 2 = 5 .
Hi, in the figure red full line and green full line values seem to be exchanged. Great explanation.
Let the radius of the red circle be r and the radius of the yellow circle be R and label the diagram as follows:
From right △ J B D with sides J B = B D = 1 , J D = 2 , and from right △ L C D with sides L C = C D = r , L D = 2 r . Since J K + K L + L D = J D , 1 + r + 2 r = 2 , which solves to r = ( 2 − 1 ) 2 .
By the kissing circles theorem on the blue, yellow, and red circles, J B 1 + M E 1 = L C 1 , or 1 1 + R 1 = ( 2 − 1 ) 2 1 , which solves to R = 2 1 .
By the Pythagorean Theorem on △ L M N , L N = L M 2 − M N 2 = ( R + r ) 2 − ( R − r ) 2 = 2 R r = 2 2 1 ⋅ ( 2 − 1 ) 2 = 2 − 2 = C E .
So A F = A D − C D + C E + E F = 2 − ( 2 − 1 ) 2 + ( 2 − 2 ) + 2 1 = 2 3 + 2 , and the area of the rectangle is A I ⋅ A F = 2 ( 2 3 + 2 ) = 3 + 2 2 .
Therefore, a = 3 , b = 2 , and a + b = 5 .