Circles in a rectangle: question 2
 In the figure, all circles are tangent to the sides of the rectangle and, with the exception of the brown circle, are tangent to each other. The black line is a common tangent of the blue, the yellow and the brown circle. The blue circle is a unit circle and the two red circles are congruent.
In the figure, all circles are tangent to the sides of the rectangle and, with the exception of the brown circle, are tangent to each other. The black line is a common tangent of the blue, the yellow and the brown circle. The blue circle is a unit circle and the two red circles are congruent.
If the radius of the brown circle can be expressed as r = c a + b , where a , b and c are integers and b is square-free, find a + b + c .
Note : Maybe it's better to try Circles in a rectangle: question 1 first.
The answer is 40.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Super! This is what I was looking for: a solution without coordinate geometry. Thank you David!
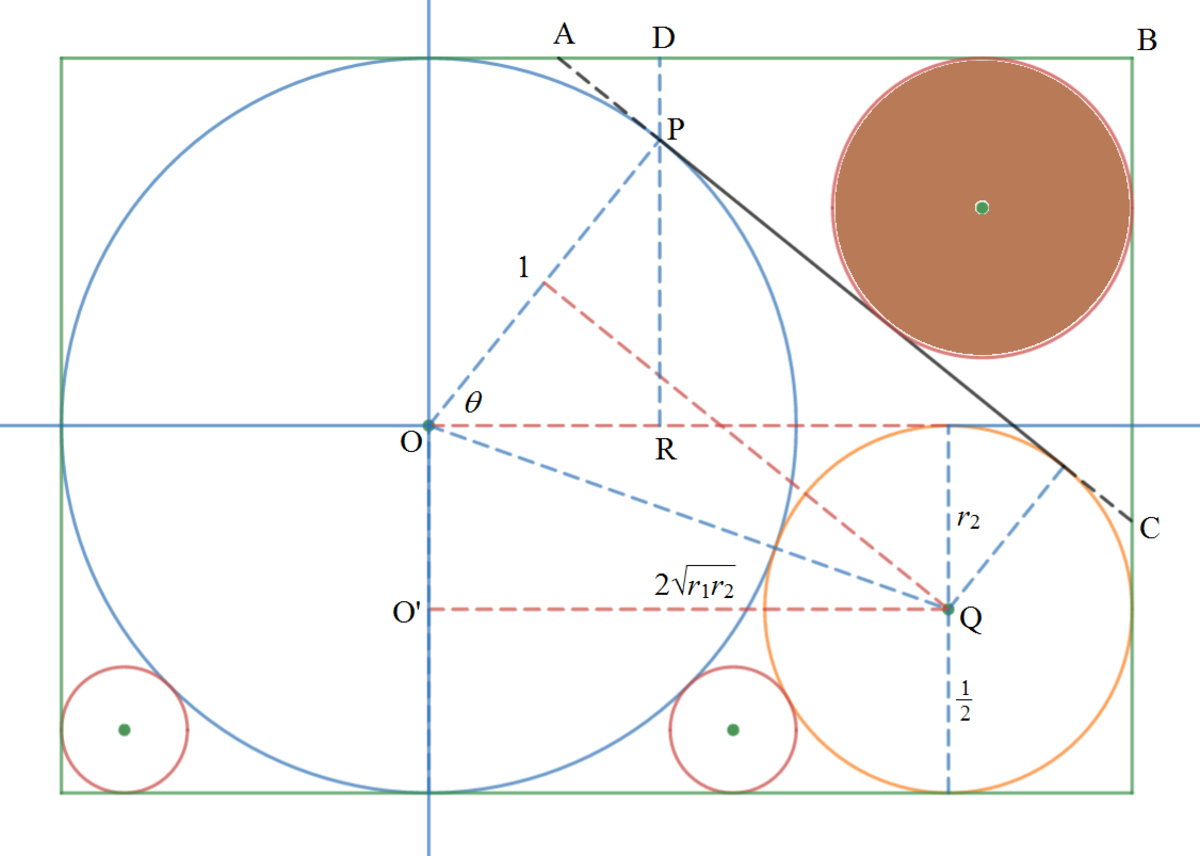
Let the center of the blue circle be the origin O ( 0 , 0 ) of the x y -plane. It is given that the radius of the blue circle r 1 = 1 . In the previous problem we found that the radius of the yellow triangle r 2 = 2 1 and the horizontal distance between the centers of blue and yellow circles O ′ Q = 2 r 1 r 2 = 2 . Then the coordinates of the right top vertex of the rectangle are B ( 2 + 2 1 , 1 ) .
Let the tangent point of the black line and the blue circle be P . Then ∠ O P R is given by:
θ = tan − 1 r 1 − r 2 2 r 1 r 2 − tan − 1 2 r 1 r 2 r 2 = tan − 1 2 2 − tan − 1 2 2 1 Note that the three red dash lines length is 2 r 1 r 2
tan θ = 1 + 1 2 2 − 2 2 1 = 4 2 7 ⟹ sin θ = 9 7 ⟹ cos θ = 9 4 2
Then P ( 9 4 2 , 9 7 ) and D P = 1 − 9 7 = 9 2 . Note that △ A D P and △ O P R are similar. Then D P A D = 4 2 7 ⟹ A D = 4 2 7 × 9 2 = 1 8 2 7 = 3 6 7 2 . And A B = 2 + 2 1 − 9 4 2 + 3 6 7 2 = 4 3 2 + 2 . Again △ A B C and △ O P R are similar and B C = 7 4 2 × A B = 7 2 ( 3 2 + 2 ) . Then C A is given by:
C A = A B 2 + B C 2 = 4 2 ( 3 2 + 1 ) 2 + 7 2 2 ( 3 2 + 2 ) 2 = 2 8 9 ( 3 2 + 2 )
The semiperimeter is as follows:
s = 2 A B + B C + C A = 2 3 2 + 2 ( 4 1 + 7 2 + 2 8 9 ) = 2 3 2 + 2 × 7 4 + 2 = 2 + 1
The are of △ A B C , A = 2 1 A B × B C = 2 1 × 4 3 2 + 2 × 7 2 ( 3 2 + 2 ) = 2 8 1 1 2 + 1 2
The brown circle is an incircle and its radius is given by:
r = s A = 2 8 ( 2 + 1 ) 1 1 2 + 1 2 = 2 8 ( 1 1 2 + 1 2 ) ( 2 − 1 ) = 2 8 1 0 + 2
Therefore a + b + c = 1 0 + 2 + 2 8 = 4 0 .
Excellent! My solution uses more coordinate geometry than yours. I wonder if we can find a purely Euclidean approach...
Log in to reply
I think it is the same. It is just that it is easier to explain. if not I have to label all the lines. Unless we do a video.
Let the radius of the red circle be r r , the radius of the yellow circle be r y , and the radius of the brown circle be r b and label the diagram as follows:
From right △ J B D with sides J B = B D = 1 , J D = 2 , and from right △ L C D with sides L C = C D = r r , L D = 2 r r . Since J K + K L + L D = J D , 1 + r r + 2 r r = 2 , which solves to r r = ( 2 − 1 ) 2 .
By the kissing circles theorem on the blue, yellow, and red circles, J B 1 + M E 1 = L C 1 , or 1 1 + r y 1 = ( 2 − 1 ) 2 1 , which solves to r y = 2 1 .
By the Pythagorean Theorem on △ L M N , L N = L M 2 − M N 2 = ( r y + r r ) 2 − ( r y − r r ) 2 = 2 r y r r = 2 2 1 ⋅ ( 2 − 1 ) 2 = 2 − 2 = C E .
That means A F = A D − C D + C E + E F = 2 − ( 2 − 1 ) 2 + ( 2 − 2 ) + 2 1 = 2 3 + 2 , B F = A F − A B = 2 3 + 2 − 1 = 2 1 + 2 , and B E = B F − E F = 2 1 + 2 − 2 1 = 2 = O M . Also, J O = J B − O B = J B − M E = 1 − 2 1 = 2 1 .
∠ J M O and ∠ J T B are corresponding angles to parallel lines, so ∠ J M O = ∠ J T B . Since T R and T E are tangent lines to the red circle, and since T M passes through the center of the red circle, ∠ R T M = ∠ M T E = ∠ J T B . Since ∠ W U Q and ∠ R T E are alternate interior angles to parallel lines, ∠ W U Q = ∠ R T E . Since U W and U Q are tangent lines to the brown circle, and since U V passes through the center of the brown circle, ∠ W U V = ∠ Q U V . Therefore, if θ = ∠ J M O , then θ = ∠ J M O = ∠ J T B = ∠ W U V = ∠ Q U V , and 2 θ = ∠ R T E = ∠ G U S .
From △ J M O , tan θ = O M J O = 2 2 1 , which means tan 2 θ = 1 − tan 2 θ 2 tan θ = 1 − ( 2 2 1 ) 2 2 ⋅ 2 2 1 = 7 4 2 .
Since △ J M O ≅ △ M T E by AAS congruence, E T = O M = 2 . Therefore, F T = E T − E F = 2 − 2 1 .
From △ T F S , S F = F T ⋅ tan 2 θ = ( 2 − 2 1 ) ⋅ 7 4 2 = 7 1 ( 8 − 2 2 ) , so G S = G F − S F = 2 − 7 1 ( 8 − 2 2 ) = 7 1 ( 2 2 + 6 ) .
From △ U G S , U G = tan 2 θ G S = 7 4 2 7 1 ( 2 2 + 6 ) = 4 1 ( 2 + 3 2 ) .
From △ U W V , tan θ = U W W V , or 2 2 1 = 4 1 ( 2 + 3 2 ) − r b r b , which solves to r b = 2 8 1 0 + 2 .
Therefore, a = 1 0 , b = 2 , c = 2 8 , and a + b + c = 4 0 .