Circles in a Triangle 01
In the figure, each of the three circles is tangent to the other two and each side of the equilateral triangle is tangent to two of the circles.
If the length of one side of the triangle is 4, what is the radius of each circle?
Details and assumptions :
∙ All the three circles have equal radii.
The answer is 0.7320.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
@Rudresh Tomar Good question. The text, though, is all in LaTeX, (at least as it appears to me). Would you be able to make it easier to read? Thanks. :)
Did it EXACTLY the same way :)
This splits the bottom side of the triangle into three parts:
2
r
and 2 parts of
r
3
.
This means that 2 r + 2 r 3 = 4 ==> r + r 3 = 2
Divide by 1 + 3 and you get
r = 1 + 3 2 = ( 1 + 3 ) ( 1 − 3 ) 2 ( 1 − 3 ) = − 2 2 − 2 3 = − 1 + 3
= 0 . 7 3 2
Really nice!
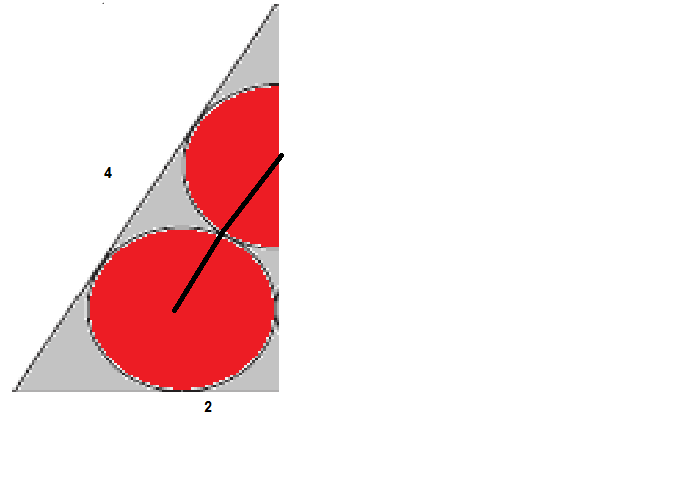 this is the exact half of the triangle .
we will be using the variable
r
for radius
this is the exact half of the triangle .
we will be using the variable
r
for radius
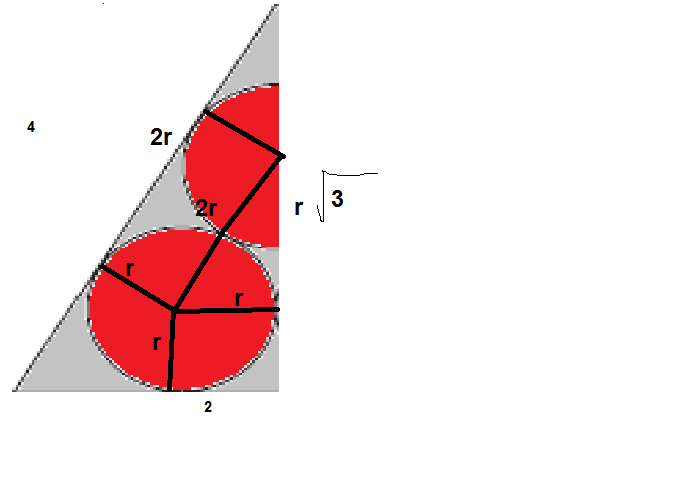 here, the
r
appear because they are from the center of the circle to a point on the circle, next,the
2
r
appear because it is the sum of the 2 radii. interestingly we have formed 3 parts that have a area that can be expressed i terms of
r
.
here, the
r
appear because they are from the center of the circle to a point on the circle, next,the
2
r
appear because it is the sum of the 2 radii. interestingly we have formed 3 parts that have a area that can be expressed i terms of
r
.
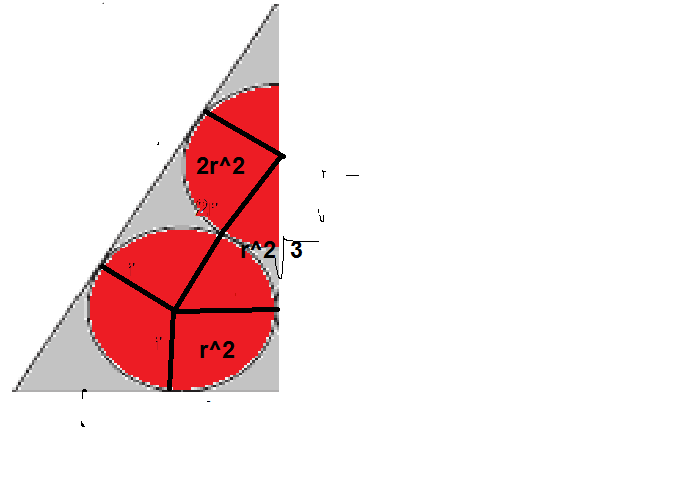 let the remaining area be x, we know the height is
2
3
by the Pythagorean theorem.
2
3
=
r
2
+
2
r
2
+
2
r
2
3
+
x
⟶
2
3
=
r
2
(
3
+
2
3
)
+
x
for x, we ca visualize, but here is a image
let the remaining area be x, we know the height is
2
3
by the Pythagorean theorem.
2
3
=
r
2
+
2
r
2
+
2
r
2
3
+
x
⟶
2
3
=
r
2
(
3
+
2
3
)
+
x
for x, we ca visualize, but here is a image
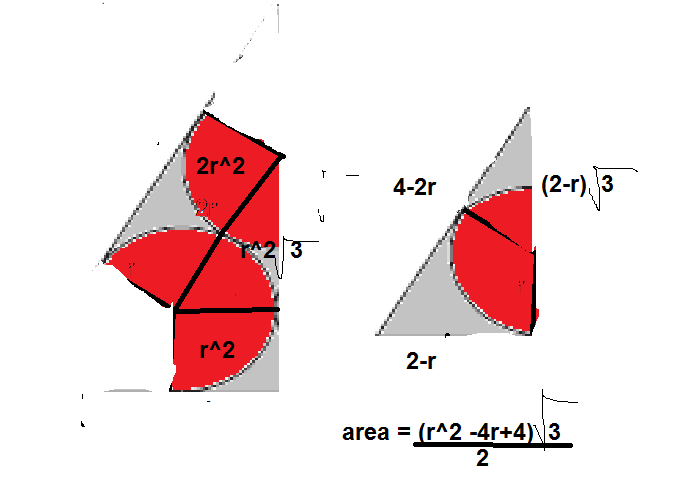 we cut it off to form a different triangle. we get the values because the whole side is 4, but we did not take the 2r, so it is
4
−
2
r
, a simlar case for
2
−
r
.
we get
(
2
−
r
)
3
by the Pythagorean theorem. now we know its area is
2
(
r
2
−
4
r
+
4
)
3
, we get that
2
3
=
r
2
(
3
+
2
3
)
+
2
(
r
2
−
4
r
+
4
)
3
→
4
3
=
2
r
2
(
3
+
2
3
)
+
(
r
2
−
4
r
+
4
)
3
6
r
2
+
2
(
r
2
−
2
r
+
2
)
3
=
4
3
⟶
3
r
2
+
(
r
2
−
2
r
+
2
)
3
=
2
3
3
r
2
+
r
(
r
−
2
)
3
=
0
⟶
3
r
+
r
3
=
2
3
r
=
3
+
3
2
3
=
0
.
7
3
2
we cut it off to form a different triangle. we get the values because the whole side is 4, but we did not take the 2r, so it is
4
−
2
r
, a simlar case for
2
−
r
.
we get
(
2
−
r
)
3
by the Pythagorean theorem. now we know its area is
2
(
r
2
−
4
r
+
4
)
3
, we get that
2
3
=
r
2
(
3
+
2
3
)
+
2
(
r
2
−
4
r
+
4
)
3
→
4
3
=
2
r
2
(
3
+
2
3
)
+
(
r
2
−
4
r
+
4
)
3
6
r
2
+
2
(
r
2
−
2
r
+
2
)
3
=
4
3
⟶
3
r
2
+
(
r
2
−
2
r
+
2
)
3
=
2
3
3
r
2
+
r
(
r
−
2
)
3
=
0
⟶
3
r
+
r
3
=
2
3
r
=
3
+
3
2
3
=
0
.
7
3
2
the picture in the solution meant 2 r 2 3 not r 2 3
From center of lower left circle drop radius, r, to base of triangle. From center of lower left circle draw line to vertex of triangle. This is the hypotenuse of a small 30-60-90 triangle and must be equal to 2 r. The third side is (4 - 2r) / 2 or 2 - r. Using Pythagoreans Theorem: (2 r)^2 = r^2 + (2 - r)^2
4r^2 = r^2 + 4 - 4r + r^2
2r^2 + 4r - 4 = 0
r^2 + 2r - 2 = 0
r = ( - 2 + sqrt ( 4 - 4*(-2)))/2 = 0.732 Note: discarded second root because it is negative.
Vivek gupta
Length of altitude of given triangle =2* \sqrt{3}
let radius be r,
sin 30=r/x, where x= dist from point A to centre of 1st circle,
i.e, x=2r
now, inner circle also form a equilateral triangle of side 2r,
Length of altitude of inner equilateral triangle is \sqrt{3} r.
then total length of altitude of triangle ABC (in terms of r)= \sqrt{3} r +2r+r
i.e., \sqrt{3}r+2r+r=2 \sqrt{3}
on solving, r=0.732
I have a different solution.
Consider the triangle spanned by the centers of the circles. It has side length 2r and each side is at distance r from the side of the original triangle that is parallel to it.
Now consider in general a triangle with all sides at distance x from the original triangle's sides. The length of its sides depends linearly on the distance x. For x=0 you get the original triangle with side length 4, and for x=4sqrt(3)/6 you get a single point, side length 0. From that you get that the formula for the side length is 4 - 2*sqrt(3)*x.
Solving the equation 4 - 2*sqrt(3)*x=2*x gives the solution, 2/(1+sqrt(3)).
Let the radius of the circles be r .
Label the lower vertices of the triangle A and B going left to right.
Drop perpendiculars from the centers of the two lower circles to the base of the triangle. Label the two points of intersection C and D , again going left to right.
Then C D = 2 r and A C = B D = 2 4 − 2 r = 2 − r .
Labeling the center of the lower left circle as O , we then have that
tan ( 6 π ) = A C O C ⟹ 3 1 = 2 − r r ⟹
3 ∗ r = 2 − r ⟹ r = 1 + 3 2 = 0 . 7 3 2 to 3 decimal places.