Circles in a Triangle 02
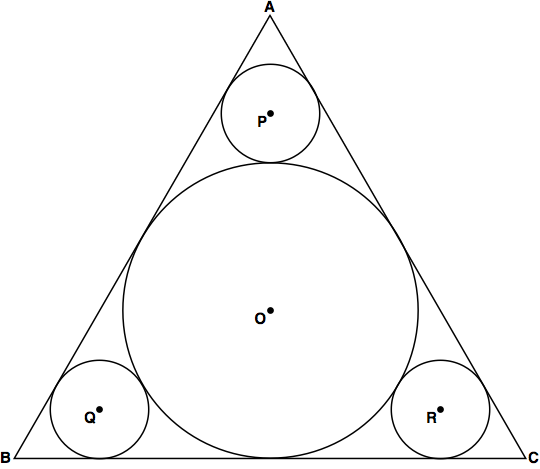 In the figure above, three small circles have equal radii of
and one big circle centered
has radius
. Given an
is equilateral. If the side of the triangle is
, then find
.
In the figure above, three small circles have equal radii of
and one big circle centered
has radius
. Given an
is equilateral. If the side of the triangle is
, then find
.
The answer is 24.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Focus first on the top circle. Let S be the point of tangency to the right side of the triangle and T the point of tangency with the big circle. Also, let X be the point of tangency of the big circle with the base of the triangle.
Now since Δ A M P is a right triangle, ∠ P A M is 3 0 ∘ and P M = r = 4 , we have that A P = 4 csc ( 3 0 ∘ ) = 8 , and thus A T = 8 + 4 = 1 2 .
Next, since O lies 3 2 the way along the median from A , we must have that A T = T O = O X = 1 2 , implying that the median length, which is also the height of the equilateral triangle, is 3 ∗ 1 2 = 3 6 .
The side of the triangle is then
a = 3 6 csc ( 6 0 ∘ ) = 3 6 ∗ ( 3 2 3 ) = 2 4 3 ,
and so 3 a = 2 4 .