Circles in Geometric Progression?
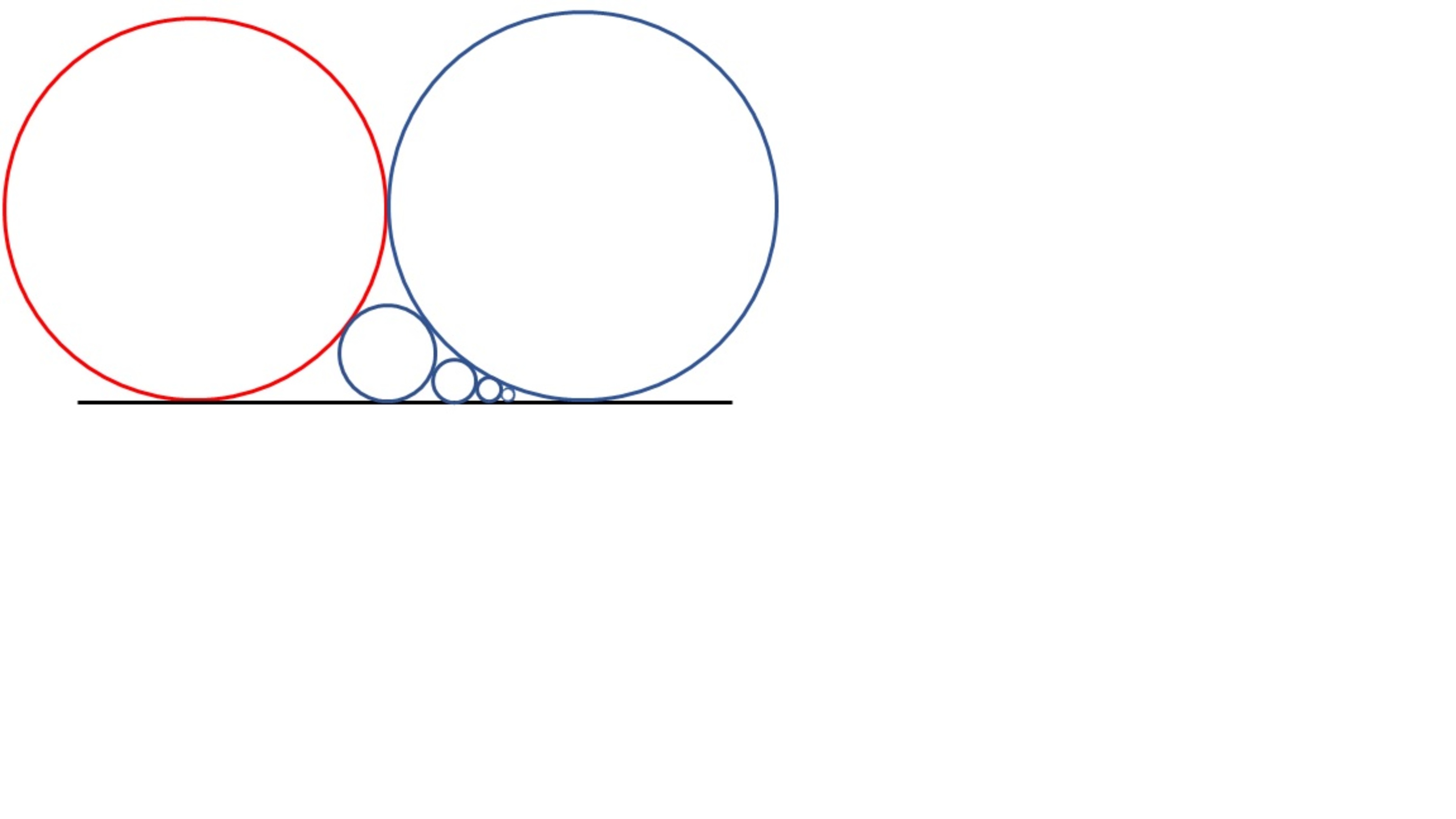
Note: The blue circles continue infinitely
The large blue and red circles have a radius of 1
If the sum of the areas of the blue circles can be writen in the form where and are integers,
What is the value of
Worded:
Let and be circles of radius touching at a point.
Let line be a line that is tangent to both and and two distinct points.
Let be the circle that is tangent to both and .
We define circle to be a circle that is tangent to and for all
If is the area of circle then where and are integers.
What is the value of
The answer is 18.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For this problem we will use the identity x 1 + y 1 = z 1 where x and y are the radii of the two larger circles and z is the radius of the smaller circle that is tangent to the two larger circles and the line which is tangent to both the larger circles. This can be easily proved geometrically.
Let r n be the radius of circle C n .
With this identity, r 1 1 + r 2 1 = r 3 1 therefore 1 + 1 = r 3 1 so r 3 = 4 1
Similarly, r n − 1 1 + r 2 1 = r n 1 for all n > 3 . (Note r 2 1 = 1 )
r 3 1 + r 2 1 = r 4 1
2 + 1 = r 4 1 so r 4 = 9 1
You can see that this pattern conitues forever so that r n = ( n − 1 ) 2 1 .
Therefore A n = π ( ( n − 1 ) 2 1 ) 2
n = 2 ∑ ∞ A n = π ( 1 4 1 + 2 4 1 + 3 4 1 . . . ) = π ζ ( 4 ) = 9 0 π 5 where ζ ( s ) is defined as the Riemann-Zeta function.
So a b = 1 8