Circles in a square!
The 5 circles have the same size. If the side of the large square is 1, what is the radius of each circle (to 3 decimal places)?
The answer is 0.183.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
14 solutions
You haven't proven that the vertical line you drew is tangent to the central circle.
Log in to reply
Of course it's a tangent, it is perpendicular to a radius.
Log in to reply
Any line is perpendicular to some radius (because a circle has a radius in every direction). To be a tangent, the point where the line and the radius meets must be on the circle.
I do think that the real question is: how do we know that the line passing from the center of the top circle and from the point of tangent of the top circle with the outer square is then tangent to the inner circle.
I mean, visually it seems so, but visually one can also make very tiny mistakes that are misleading.
Who say that the vertical tangent line is crossing the center of the upper circular ?
Log in to reply
Good question, Hassan! Right off hand I can't prove it, but it must.
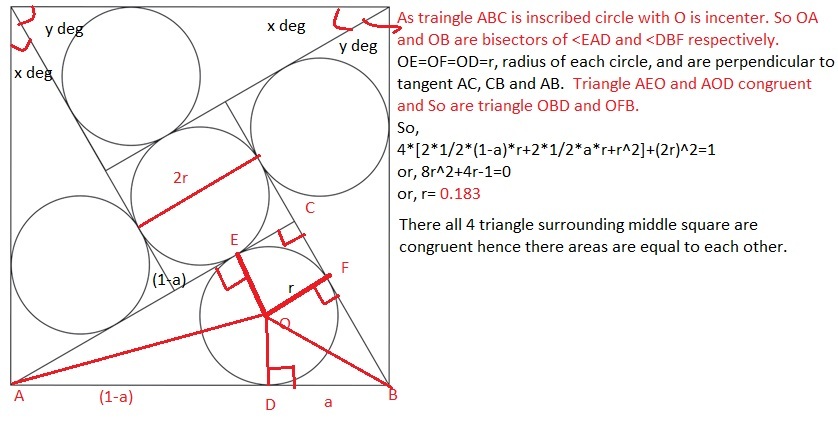
here is a simple solution by area calculation: let A be the part of the square size between any vertex and the closet congruent point of the closest circle. with A and r we can calculate the area of the triangle that is built on this size, by summing up 2 kites and the small square: small kite = A r big kite = (1-A) r small square = r^2 there are 4 such triangles + the square in the middle we get: 4(A r+(1-A) r+r^2) + 4 r^2 = 1 simplify to eliminate A and get: 8 r^2 + 4*r - 1 = 0
where did you get your third equation from?
Log in to reply
sqrt ((2r)^2 - r^2) = sqrt (4r^2 - r^2) = sqrt (3r^2) = r * sqrt (3) = sqrt (3) *r :)
I didn't feel like doing it, so I guessed the answer would be 0.2. So, close. :(
How can you say that the line passing horizontally through the centre of the circle bisects the side of the square??
according to you, r = 1/2 - x that mean r = - 1.23 which does not fit at all ...
Log in to reply
Actually the x=[sqrt(3)]*r So you missed out the r when you substitute x into the first equation.
Nice solution. i was making this complicated :3
Let be a, b, c, the ordered sides and hypotenuse of every right angled triangle. The center of every inscribled circle in the rispective triangle is de incenter of the triangle whic is the point of intersection of the bisectors of every angle. Let be A, B, C the angles opposite to a, b, c, with c = 1, C = Pi/2; we have: Pi/4 - A = A/2; => A = Pi/6, so: a = c*sinA = sinA, because c = 1; a = r + rcosA + r(1 + sinA)sinA/cosA; => r = sin(A)/(1 + cosA + tanA(1 + sinA)); A = Pi/6, => sinA = 1/2; cosA = sqrt(3)/2; tanA = sqrt(3)=> r = 1/(2(1 + sqrt(3)) = 0.183012701
My solution would start by assuming that the triangles are 30-60 right triangles. From there, the area of each triangle would be [sqrt(3)/8] multiply it by 4 then subtract it to the area of the large square. Take the square root of the answer, that gives you the side of the small square. Then divide it by 2 for the radius.
Log in to reply
You cant assume that its a 30 by 60 triangle. You have no proof
wrong concept
remarkable solution!!!!!!! it took me 15 min. to solve it due to the complicated algebra i got into and that too in three(x,y,r) variables
Let r be the radius of the circle, a be the short leg, and b be the long leg. From the diagram, we can tell that 2 r = b − a . There is a well known relation for the radius of a circle inside a right triangle: r = 2 1 ( a + b − c ) .
We equate the two and discover that a = 2 1 . From here, the solutions for b and r are obvious.
This is not as elegant as Michael Mendrin's proof without words, but it is short.
Zheng, you may be modest, but I think yours is the fastest way to prove the answer without a lot of hand waving.
I like this problem. It is a twist to the Chinese proof (which was rediscovered by Bhaskara).
Exactly Same Way.
how you said that 2r = b - a
Log in to reply
2r is the side length of the smaller square, which is equal to the length of the larger leg minus the smaller leg of the right triangle..
 image
image
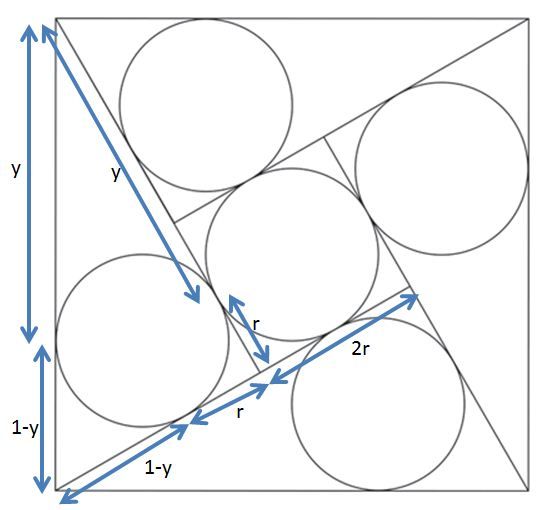
Let r be the radius of the circle.
From a point we can draw two tangents to circle and both will be of same length.
From diagram, there are four Right angle triangles and all are congruent.
The Hypotenuse of the triangle is 1. Assume the length of the tangent from the top left point of the square to the left bottom circle is y . the other part of the hypotenuse will be 1 − y
The sides of one triangle looks as in the figure attached.
The longest side can be ( ( 1 − y ) + r + 2 r ) or ( y + r )
i.e., 1 − y + 3 r = y + r
i.e., y = 2 1 + r
The longer side of the triangle is 2 1 + 2 r and shorter side is 2 1
Applying pythagoras theorem for the right angle triangle, you will get below quadratic equation,
8 r 2 + 4 r − 1 = 0
solving the equation, r = 0 . 1 8 3 or − 0 . 6 8 3
Radius should be > 0
Therefore answer is 0 . 1 8 3
Best answer
Best solution ever.
What a solution!
Thank you for not assuming and actually showing real measurements. Circles within angles have legs that are equal in length.
Here's a "proof without words" graphic. After staring at this a bit, you can already make out the answer to this problem. No need for complicated algebra involving two variables, or even one.
 Circles In Square
Circles In Square
Thanks! I added that into the question.
The image looks simple. I don't have a non-crude/brute force way. Thoughts?
Log in to reply
say shorter side length of each right angled triangle is x, the other 2 sides are of length 1 and 2r+x. By pythagoras thm. x^2+(2r+x)^2=1 => 2(x^2)+4xr+4(r^2)=1 => 4xr+4(r^2)=1-2(x^2) (1) And, to quote you "The area of an individual triangle is given by the inradius multiplied by the perimeter, divided by 2" which is 4xr+2(x^2)= 2r+4xr+4(r^2) (2) using (1) =>4xr+2(x^2)= 2r+1-2(x^2) =>rearranging and adding r^2 on both sides =>4(x^2)+4xr+r^2=r^2+2r=1 since all values are positive, taking square root, 2x+r=r+1 x=0.5 Now, the side of length 2r+x is also equal to sqrt(1-x^2) substituting x=1/2, we get r=(root3-1)/4=0.183
Log in to reply
The shorter side length of each right angled triangle is 2 r , the hypotenuse is 4 r , and therefore the other length is 2 3 r . ( 2 3 + 2 ) r = 1 ⟹ r = 0 . 1 8 3 . . . . Of course, this graphic needs some proving...
this seems like a graphic without proof to me. It doesn't seem at all clear.
The link is broken. Can you fix it please?
Do you mean 1 0 0 % = 1 that 1 is the answer?
ACAD IS THE PROOF
By looking at the diagram it is clear that the four triangles are congruent and and also right angled. It is given to us that the hypotenuse of each of these 4 triangle is equal to 1.
Let the longer side of each of the right triangle be 2c and the shorter side be 2b. Now clearly the length of each of the side of the smaller square in the center of the diagram is 2c - 2b which is also the diameter of each of the circle. That means that the radius of each circle can be represented as c-b.
Using the property that the tangents drawn from an external point to a circle are congruent , we can find that the lengths of all the remaining segments of the right triangle that are tangent to the circle and represent the hypotenuse of each of the right triangles as 4b.
But as it is given to us that each side of the large square is 1, therefore we get that:
4b =1
b = 1/4
2b = 1/2 ( shorter side of the right triangle in the given diagram)
We can use the pythagorean theorem to find that 2c is approximately equal to 0.866.
The diameter of the circle (2c - 2b) is therefore 0.866 - 0.5 = 0.366.
Finally dividing that be 2 we get the radius of the circle as 0.183.
hw did u get 1=4b?
Here is the solution applying inscribed circle and in-center rule.
(cos 30 (deg) X 1 = .8660254)-(sin 30(deg) *1 =.5) = .3660254 (sides of small square) / 2 =.1830 radius of circle
Great answer
Log in to reply
This is how I did it but I am still not sure that I can PROVE that it is a 30 60 90 triangle. though I convinced myself it must be..lol

In the diagram we can observe two main values: x and y , which are distributed along all the triangles due to the tangential points properties. We can observe that k = 2 x + y , and because k + y = 1 ⟹ x + y = 2 1 . Now we can also find that the remaining side length of the right triangle is 2 3 , which gives us the following system of equations:
x + y = 2 1 3 x + y = 2 3
Where we only solve for x since it is the radius of the circle:
x = 4 3 − 1 ≈ 0 . 1 8 3
The triangles are 30-60-90 right triangles, which always have the same ratio:
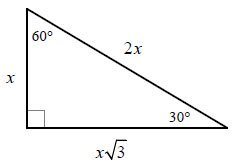 Since we know that the hypotenuse of the triangle is 1, we can say that the side opposite the
3
0
∘
angle is .5, and the side opposite the
6
0
∘
angle is
.
5
3
Since we know that the hypotenuse of the triangle is 1, we can say that the side opposite the
3
0
∘
angle is .5, and the side opposite the
6
0
∘
angle is
.
5
3
The length of the side of the smaller square + .5 = . 5 3 . 5 3 - .5 = .366 (the diameter of the circle)
.366 / 2 = .183
How do you know that it was a 30-60-90 triangle in the first place?
Let the radius of the circle be r . By symmetry, (assume that) the triangles are equal. Let the length of the shorter leg be l , which makes the length of the longer leg l + 2 r . From the right angled triangle, we get that
l 2 + ( l + 2 r ) 2 = 1 .
The area of an individual triangle is given by the inradius multiplied by the perimeter, divided by 2, which is r × ( 1 + l + l + 2 r ) ÷ 2 . Thus, the area of the large square, viewed as the area of the 4 triangles plus the small center square, gives us
1 = 2 r ( 1 + 2 l + 2 r ) + ( 2 r ) 2 .
With these 2 equations, I couldn't figure out an easy way to deal with them, so I threw it into Wolfram. The only reasonable solution, where 0 < l < 1 and r > 0 was l = 2 1 , r = 4 1 ( 3 − 1 ) ≈ 0 . 1 8 3 .
If anyone knows how to deal with those equations, please let me know!
Here's a "proof without words" graphic. After staring at this a bit, you can already make out the answer to this problem. No need for complicated algebra involving two variables, or even one.
 Circles In Square
Circles In Square
Log in to reply
I don't understand how you use this graphic to solve the problem without variables. Can you explain your solution, please?
Which program did you use to draw this?
Log in to reply
Mathematica. I've been using Mathematica since the 1990s, when I did image processing work.
I followed the same approach as Calvin but stopped at the point of using online tools such as mathematica since i am not sure about the capabilities that are made publicly available
I did think about the rotation alternative but did not follow it up
Let a, b, c, be the ordered sides and hypotenuse of every right angled triangle. The center of every inscribled circle of radius r in the rispective triangle is the incenter of the triangle whic is the point of intersection of the bisectors of every angle. Let A, B, C, be the angles opposite to a, b, c, with c = 1, C = Pi/2; we have: Pi/4 - A = A/2; => A = Pi/6, so: a = c*sinA = sinA, because c = 1; a = r + rcosA + r(1 + sinA)sinA/cosA; => r = sin(A)/(1 + cosA + tanA(1 + sinA)); A = Pi/6, => sinA = 1/2; cosA = sqrt(3)/2; tanA = sqrt(3)=> r = 1/(2(1 + sqrt(3))) =(sqrt(3) - 1)/4 = 0.183012701
I "solved" it by letting the shorter sides of the triangle as b and c. "Solved", because I forgot to divide b - c by 2. :( First, b 2 + c 2 = 1 Then, equating the incircle radii, 1 + b + c b c = 2 b − c 2 b c = b − c + b 2 − c 2 2 b c = b − c + 1 − 2 c 2 ( 2 c − 1 ) b = ( 1 + c ) ( 1 − 2 c ) ( 2 c − 1 ) ( 1 + b + c ) = 0 Hence, c = 2 1 And, b = 2 3 r = 4 3 − 1 = 0 . 1 8 3
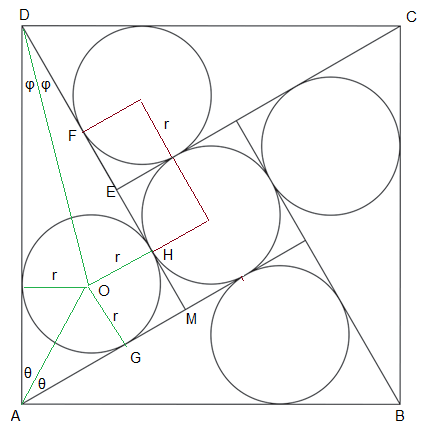
- 2 ( θ + φ ) = π / 2 or θ + φ = π / 4
- O H / D H = r / D H = t a n φ or D H = r c o t φ
- Similary A G = D F = r c o t θ because triangle ADM and CDE are congruent
- D H − D F = r c o t φ − r c o t θ = 2 r or c o t φ − c o t θ = 2 or t a n θ − t a n φ = 2 t a n θ t a n φ
- t a n φ = t a n ( π / 4 − θ ) = ( 1 − t a n θ ) / ( 1 + t a n θ )
- Substituting and solving will give 3 t a n 2 θ − 1 = 0 or t a n θ = 1 / √ 3 or θ = π / 6
- Therefore the ADM is 30-60-90 right angled triangle (Note that angles are 2θ and 2φ)
- A D s i n π / 3 = 1 / 2 = r ( 1 + c o t π / 6 ) or r = 1 / ( 2 ( √ 3 + 1 ) ) = 0 . 1 8 3
We have inner circlle right triangle raduis r = 2 a + b − c (0) also we have four equal triangles and one square inside surface of bigger square so the sum of four triangles and little square is - 2 a × b + 2 a × b + 2 a × b + 2 a × b + ( 2 × r ) 2 = c 2 - and we know that c = 1 and c 2 is area of bigg square so we have 2 × a × b + ( 2 × r ) 2 = 1 (1) then because triangles are rectangular we have a 2 + b 2 = c 2 and when we change c = 1 we get a 2 + b 2 = 1 (2) then we eqal left sides of expresion (1) and expresion (2) (because right sides are equal to 1 ) then we get 2 × a × b + ( 2 × r ) 2 = a 2 + b 2 (3) then expresion (3) becomes a 2 + b 2 − 2 × a × b = ( 2 × r ) 2 and further we have ( a − b ) 2 = ( 2 × r ) 2 (4) so if we do square root of expresion (4) we get - a − b = 2 × r (5) . Now we go back to expresion (0) r = 2 a + b − c and multiplicate it by 2 and we know c = 1 so we get a + b − 1 = 2 × r (6) now if we equal left sides of expresions (5) and (6) we get a − b = a + b − 1 so 2 × b = 1 and then b = 2 1 now we can find (a) from a 2 + b 2 = 1 so a 2 + ( 2 1 ) 2 = 1 then a 2 = 4 3 and finaly a = 2 3 . We have a = 2 3 , b = 2 1 and c = 1 so we can find ( r ) from r = 2 a + b − c so r = 2 2 3 + 2 1 − 1 = 0 . 1 8 3
Did it with pythagoras and then I devided equal lines in 3 parts. I did this without angles. I took the side 1 and the other side as 1/2.
The radio is a simple function of the area of the small square (in the center). The area of each of the four triangles is simple to calculate. The smal square area is equal to the large square (1) minus four triangles.
How is the area simple to calculate unless you assume they are 20-60-90 triangles.??? If you are allowed this assumption your solution is more simple than mine. I did assume a 30-60-90 triangle. starting at the lower left corner as A and going clock wise B,C,D. If we extend the line leaving B thru point C to a point X outside the square; Its length determined by tan 30 =opp/adj where opp= 1 ; then the extended line from B X = 1 /tan 30 ;BX = 1.732. Now BC = 1; 1.732 -1 = CX = 0.732 . This point X is where the line going from A up and to the right of point C if extended meets Now if we draw a parallel line thru the centers of of the 3 circles it will intersect the CX (the extended portion of BC ) bisecting the 0.732 /2 = 0.366; now we have a 30 deg angle where the hypotenuse is = 0.366 So Sin 30 = opp / hyp and opp=sin 30 (hyp); =sin 30 x 0.355 ; = 0.5 x 0.366 or 0.183 = the radius
Having assumed the triangles to be 30-60-90 and solving the problem. Will go a step farther and state that 30-60-90 triangles are the only triangles that allow the circles orientation within the square. (i.e. the circles touch all sides of the individual triangles and the one square.
r + x = 1/2
x = sqrt ((2*r)^2 - r^2)
x = sqrt(3)*r
r = 0.183