Circles Inside a Larger Circle
 We inscribed circles in a larger circle. Circles of the same color are congruent.
Given the radius of one of the blue circles as
5
, what is the radius of the pink circles?
Please round your answer to the nearest whole number.
We inscribed circles in a larger circle. Circles of the same color are congruent.
Given the radius of one of the blue circles as
5
, what is the radius of the pink circles?
Please round your answer to the nearest whole number.
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Thank you for sharing your solution.
Nice solution, I used this only!
We apply Descartes' theorem here. Let the radius of the pink circle be r . Then by this theorem,
r 1 = − 1 0 1 + 5 1 + 5 1 −
2 − 5 × 1 0 1 + 5 × 5 1 − 5 × 1 0 1 = 1 0 3
⟹ r = 3 1 0 ≈ 3 . 3 3 .
So the required answer is 3 .
Thank you for sharing your solution.
Thank you for sharing your solution, same as mine in the video, but there is no need to remove it. All solutions are welcomed.
This was my latest YouTube Video Problem, I started this channel last week. I am open minded to any kind of comments for improvement purposes.
Here's the solution: Solution
Great Channel Hana! And nice problem as well!
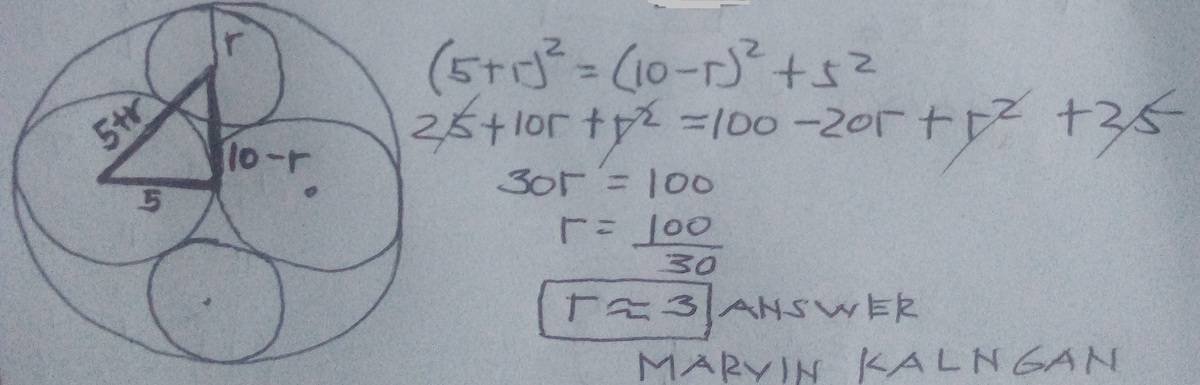
We note that the radius of the large circle is 1 0 and that
r + ( r + 5 ) 2 − 5 2 r + r 2 + 1 0 r r 2 + 1 0 r r 2 + 1 0 r 3 0 r ⟹ r = 1 0 = 1 0 = 1 0 − r = 1 0 0 − 2 0 r + r 2 = 1 0 0 = 3 1 0 ≈ 3