Circles, Isosceles Right Triangles and Squares
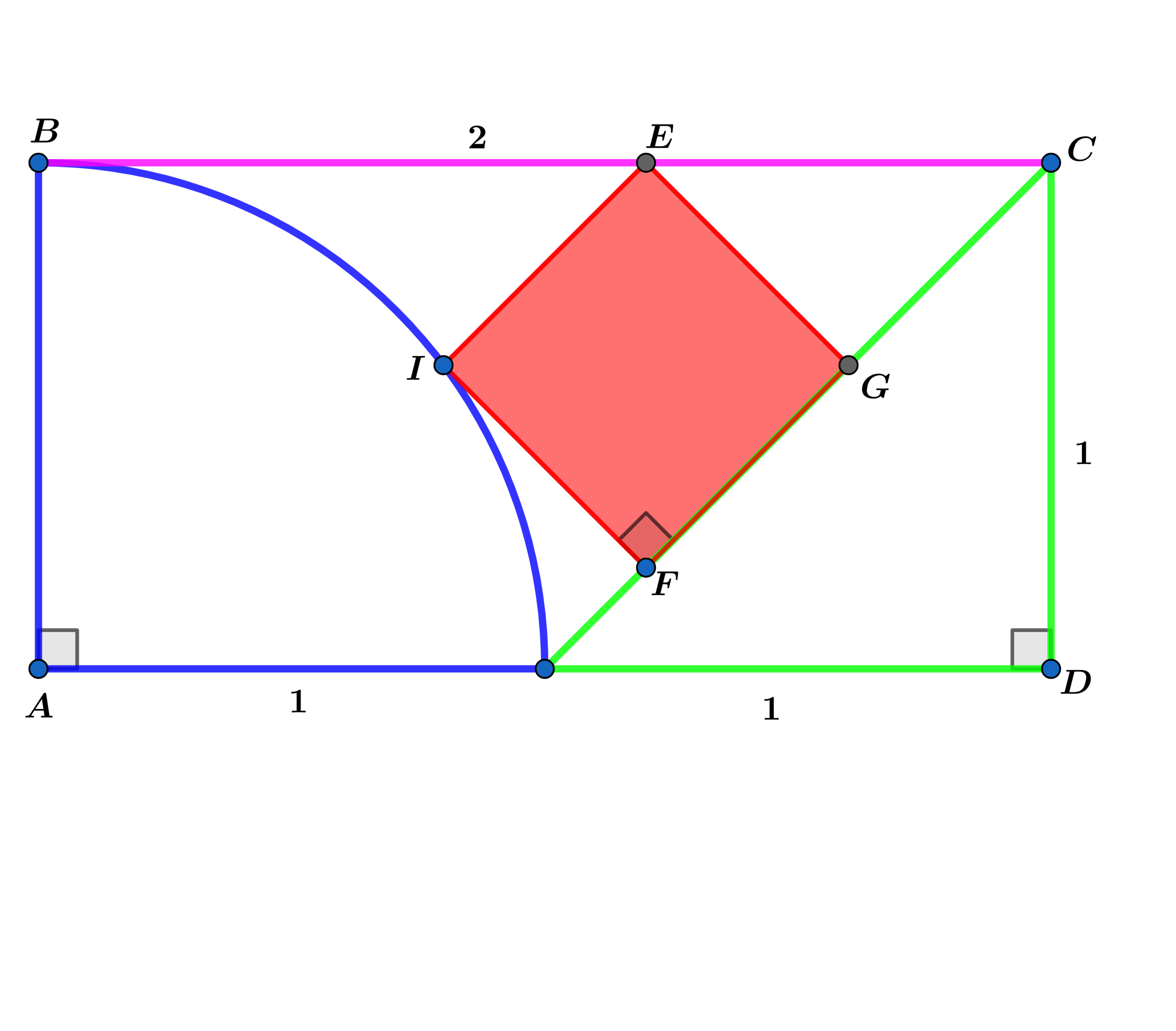
A quarter of a circle with radius 1 , an isosceles right triangle with side length 1 and a square are inscribed in a 2 by 1 rectangle as shown above.
If the area A s of the square is A s = b a , where a and b are coprime positive integers, find a + b .
The answer is 33.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
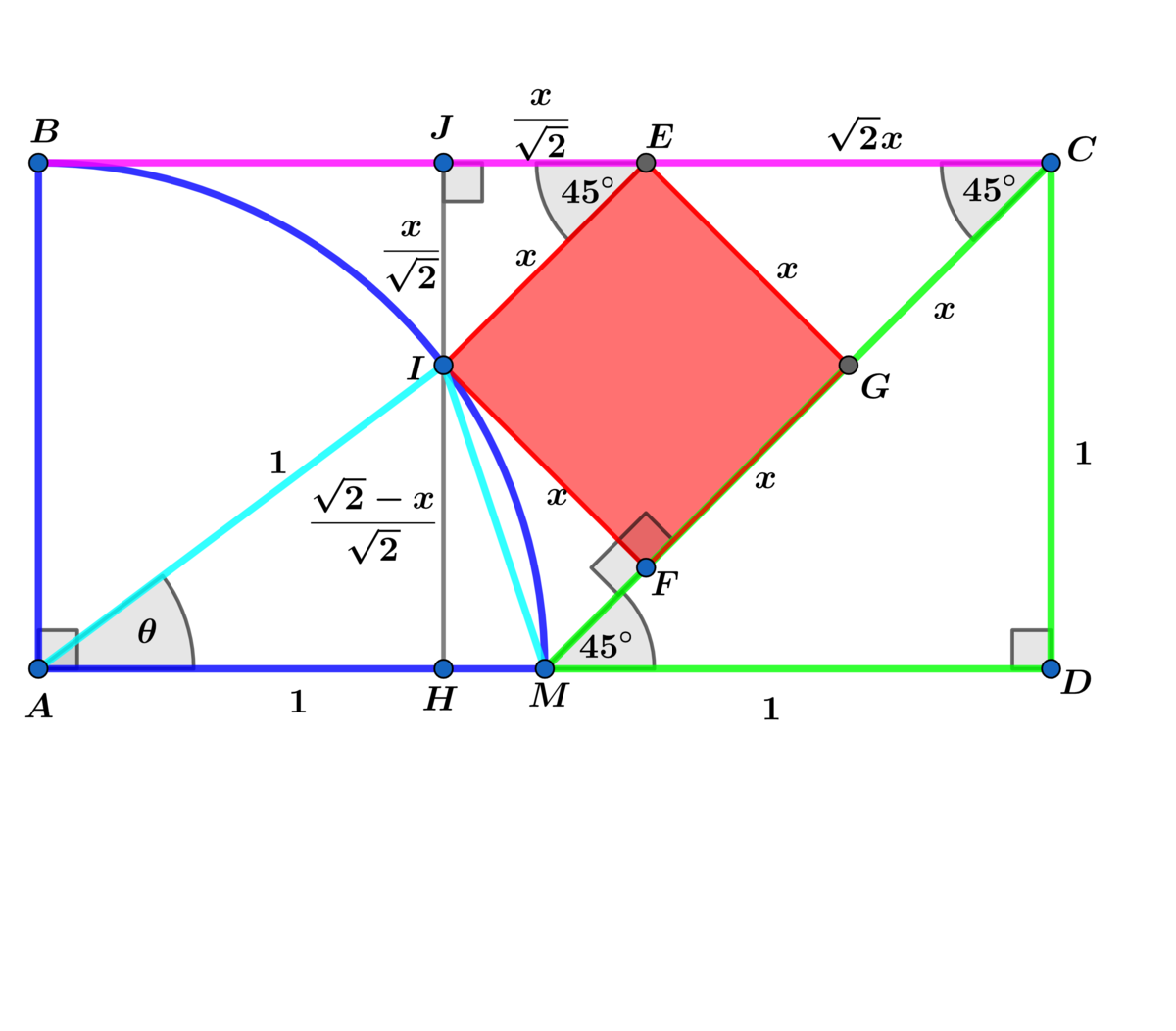
Using the above diagram:
M C = 2 and B E = B C − E C = 2 − 2 x ⟹ A H = B E − J E = 2 2 2 − 3 x
= cos ( θ ) and M F = M C − F C = 2 − 2 x
Using the law of cosines on △ A I M ⟹ I M 2 = 2 ( 1 − cos ( θ ) ) = 3 2 x − 2
Using the Pythagorean theorem on △ I F M ⟹ x 2 + ( 2 − 2 x ) 2 = 3 2 x − 2
⟹ 5 x 2 − 4 2 x + 2 = 3 2 x − 2 ⟹ 5 x 2 − 7 2 x + 4 = 0 ⟹
x = 1 0 7 2 ± 3 2 = 2 , 5 2 2 and x = 2 ⟹ x = 5 2 2 ⟹ A s = 2 5 8
= b a ⟹ a + b = 3 3 .
If we draw a rectangle with diagonal IC and sides parallel to the rectangle ABCD, it's easy to see that the ratio of its sides is 3 to 1 (using Rocco's diagram as reference, this rectangle would be IJCK, with K being the intersection point of extrapolated line IG & CD). All we need to do is applying Pythagoras to find the width / height (noted as x) and the area would be double of its square (in fraction form) and finally the answer will appear after summing the nominator and denominator together.
(1 – x)² + (2 – 3x)² = 1²
10x² – 14x + 5 = 1
10x² – 14x = 1 – 5
(x – 0.7)² = 0.7² – 0.4 = 0.09
x = 0.7 ± √0.09
= 0.7 ± 0.3
Since 0 ≤ x < 1, x = 0.4
Area
= 2x²
= 2 × (2/5)²
= 8/25
Answer
= 8 + 25 = 33
Let the midpoint of A D be O , the origin, let H be the center of the square, and let F have coordinates F ( k , k ) .
Then E F = 1 − k , so E H = H I = 2 1 ( 1 − k ) , which means I has coordinates I ( k − 2 1 ( 1 − k ) , k + 2 1 ( 1 − k ) ) = I ( 2 3 k − 2 1 , 2 1 k + 2 1 ) .
I is also on the quarter circle ( x + 1 ) 2 + y 2 = 1 , so ( 2 3 k − 2 1 + 1 ) 2 + ( 2 1 k + 2 1 ) 2 = 1 , which solves to k = 5 1 .
The area of the square is then 2 1 E F 2 = 2 1 ( 1 − k ) 2 = 2 1 ( 1 − 5 1 ) 2 = 2 5 8 , so a = 8 , b = 2 5 , and a + b = 3 3 .