Circles may help?
If the maximum value of S = ( 1 − x 1 ) ( 1 − y 1 ) + ( 1 − x 2 ) ( 1 − y 2 ) is ( c + k ) 2 and x 1 2 + x 2 2 = y 1 2 + y 2 2 = c 2 , where c is some positive number.
Find k ! .
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
My solution needs no help of circle.
Just use the following facts for all** a and b belong to real to find the maximum
Max(ab)=(a^2+b^2)/2
Max(a+b)=√2*√(a^2+b^2)
Setting X1 as Ccostheta and X2 as Csintheta And Y1 as Ccosalpha and Y2 as Csinalpha Easily yields the maximum value
It's easy said than done. Could you please show your "easy" solution for everyone to see? Fan of Fujinuma huh?
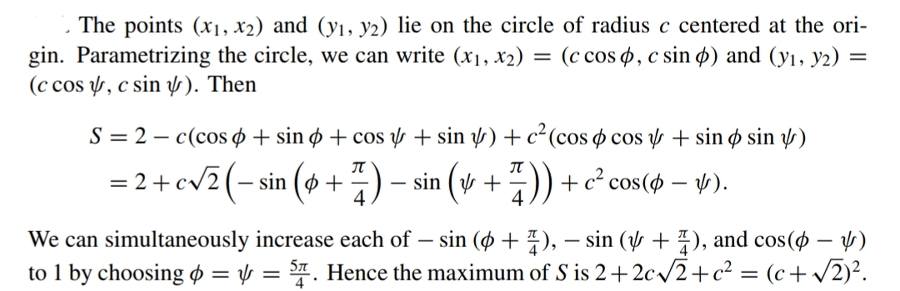
Set z 1 = 1 + i , z 2 = x 1 + i x 2 , z 3 = y 1 + i y 2 , z 0 = ( z 1 − z 2 ) ( z 1 − z 3 ) Then S = Re ( z 0 ) ≤ ∣ z 0 ∣ ≤ ( c + 2 ) 2 and equality occurs when z 2 = z 3 = − ( 2 c + i 2 c ) . Inequality above follows from triangle inequality.