Circles wont work

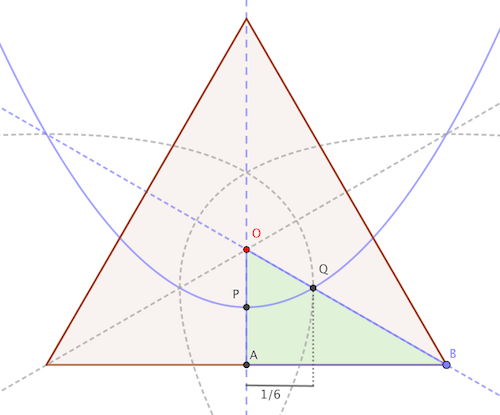
The points of the triangle that are at the same distance from the centroid and each side must lie on a parabola . The guitar-pluck-like shape formed by the intersection of the three parabolas contains all the points that are closer to the centroid than to its sides. Let's call $S$ the area of this region and $T$ , the area of the triangle. The probability we are looking for is $p=\frac{S}{T}$ . By symmetry, this ratio can be obtained by calculating the areas of the regions $OPQ$ and $OAB$ .

Consider a triangle of side $1$ and write all coordinates with respect to $A$ . The position of its centroid is $(0,\frac{\sqrt{3}}{6})$ and the vertex of the parabola lies at $(0,\frac{\sqrt{3}}{12})$ .

The equations of line $OB$ and parabola $PQ$ are:

$\begin{aligned} \text{line }OB: y&=&\textstyle \frac{\sqrt{3}}{6}(1-2x) \\ \text{parabola: }y&=&\textstyle \sqrt{3}(x^2+\frac{1}{12}) \end{aligned}$

These two curves intersect at $x=\frac{1}{6}$ .

The area $OPQ$ is given by the integral $\displaystyle \int_{0}^{\frac{1}{6}} \textstyle \left[ \frac{\sqrt{3}}{6}(1-2x) -\sqrt{3}(x^2+\frac{1}{12})\right ]\,dx=\dfrac{5\sqrt{3}}{648}$

and the area of triangle $OAB$ is $\dfrac{\sqrt{3}}{24}$ .

Finally, $p=\dfrac{\text{area } OPQ}{\text{area }OAB}=\boxed{\dfrac{5}{27}}$

Just take 3 parabolas with centroid as d focus n side as directricz..