Circuit City

Electricity and Magnetism Level 2

Circuits are powered by a 9 volt battery and current flows through a combination of resisters as shown in diagram. What is the current flowing in branch line F-C in amperes? The resisters are labeled in units of ohms. Provide your answer to the nearest 1/1000th.


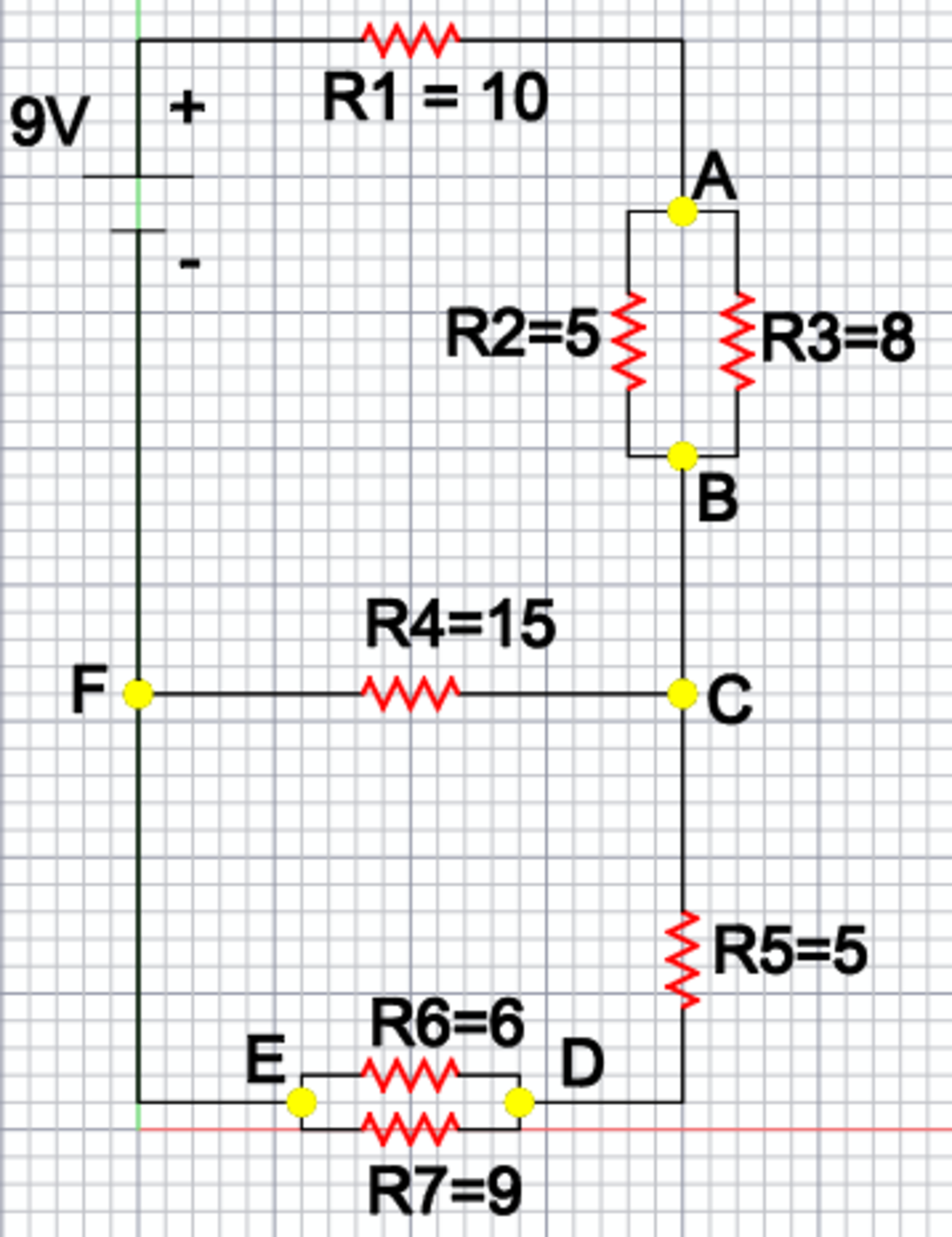
The answer is 0.177.

A Former Brilliant Member by A Former Brilliant Member

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

K T
Jan 31, 2021

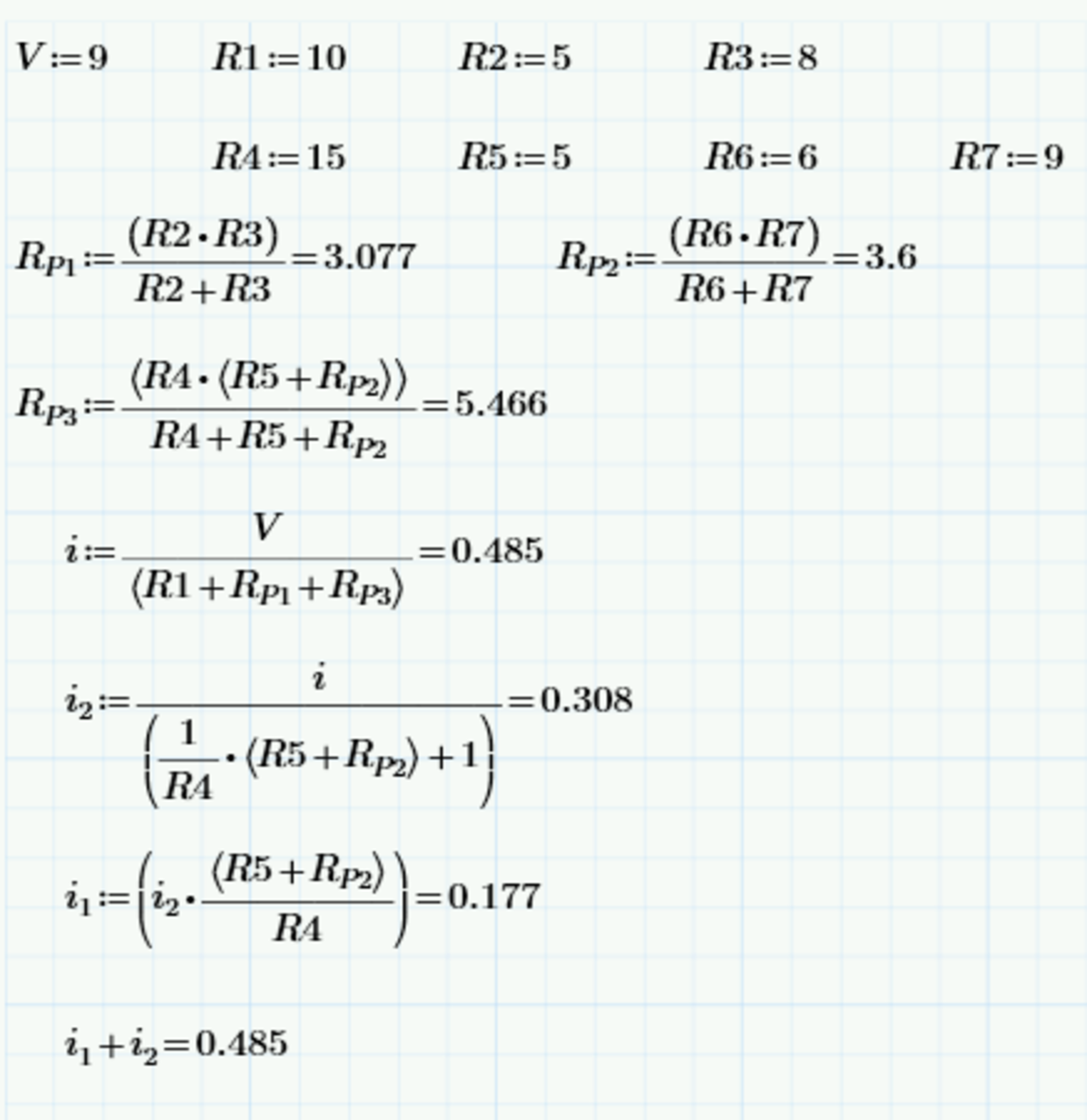
Parallel resistors combine as R = R 1 R 2 R 1 + R 2 R=\frac{R_1R_2}{R_1+R_2} .

Therefore R A B = 5 × 8 5 + 8 = 40 13 R_{AB}= \frac{5×8}{5+8}=\frac{40}{13} and R D E = 6 × 9 6 + 9 = 18 5 R_{DE}= \frac{6×9}{6+9}=\frac{18}{5} . Between F and C we have 5 + 18 5 = 43 5 5+\frac{18}{5}=\frac{43}{5} in the lower branch and 15 in the upper branch (R4). Combined this is 645 118 \frac{645}{118}

The total resistance R = 10 + 40 13 + 645 118 = 28445 1534 R=10+\frac{40}{13}+\frac{645}{118}=\frac{28445}{1534} and so the total current equals I = V / R = 13806 28445 I=V/R=\frac{13806}{28445}

The current splits according to the inverse of the resistance, so through R4 flows 43 118 I \frac{43}{118} I and through R5 flows 75 118 I \frac{75}{118} I .

The requested answer therefore is 43 118 × 13806 28445 = 296829 1678255 ≈ 0.17687 A \frac{43}{118}× \frac{13806}{28445}=\frac{296829}{1678255}\approx 0.17687 A

1 Helpful 1 Interesting 1 Brilliant 0 Confused

0 Helpful 1 Interesting 0 Brilliant 0 Confused

Should be listed as an E&M prob instead of Classical Mechanics.

tom engelsman - 4 months, 1 week ago

Log in to reply

Thanks for spotting that. Will change.

A Former Brilliant Member - 4 months, 1 week ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...