Circuits
Electricity and Magnetism
Level
2
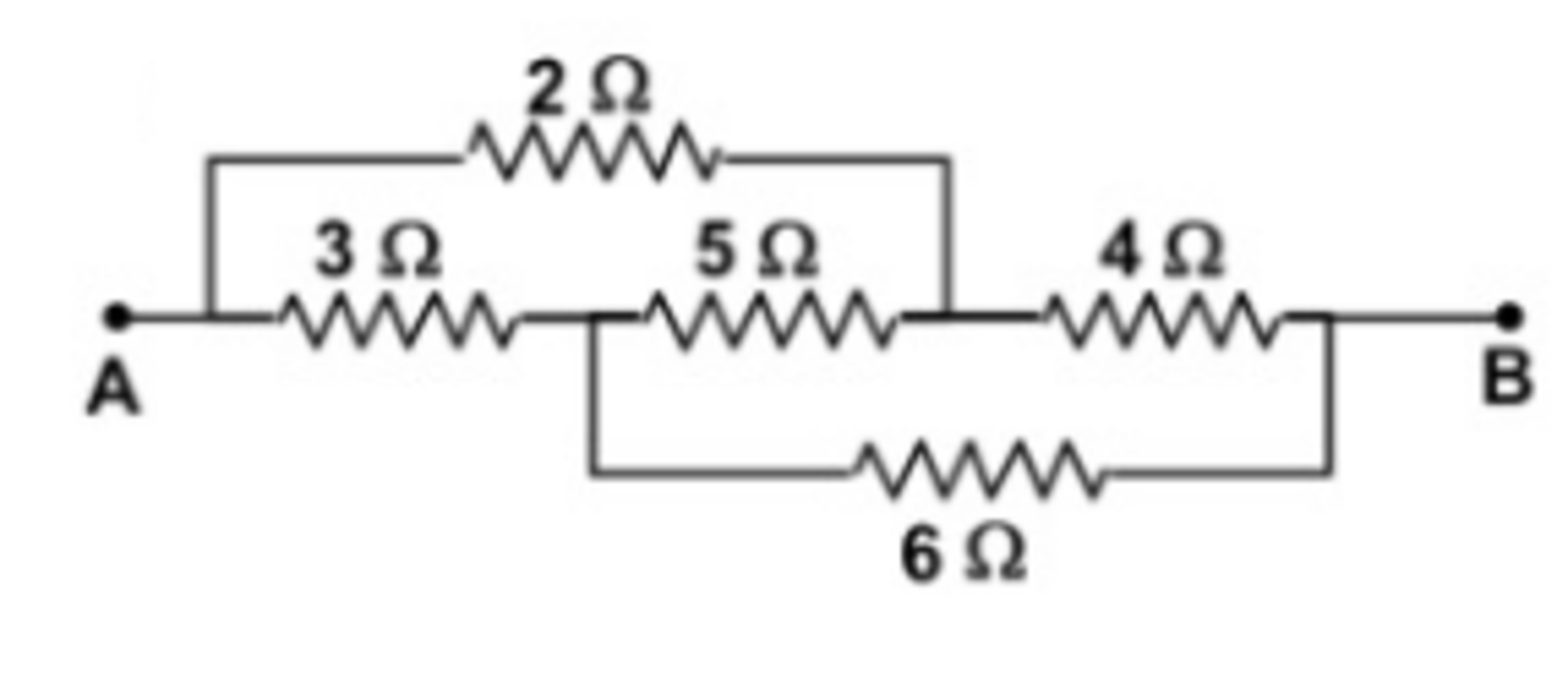
In the circuit shown, some potential difference is applied between A and B. Find the equivalent resistance between A and B.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The circuit shown can be redrawn to be as the circuit above. Let the voltage between A and B be V A B . Then the voltages at points C and D , V C B and V D B respectively, by voltage division, are:
V C B V D B ⟹ V C B = 2 + 4 4 V A B = 3 2 V A B = 3 + 6 6 V A B = 3 2 V A B = V D B
Open Circuit: Since there is no potential difference between C and D , there is no current flowing through the 5 Ω resistor, which can thus be replaced by an open circuit. Then the equivalent resistance between A and B is:
R A B = ( 2 + 4 ) ∣ ∣ ( 3 + 6 ) = 6 ∣ ∣ 9 = 6 + 9 6 × 9 = 5 1 8 Ω
Short Circuit: Since points C and D have the same potential, the 5 Ω resistor can be considered as a short circuit. Then the equivalent resistance between A and B is:
R A B = ( 2 ∣ ∣ 3 ) + ( 4 ∣ ∣ 6 ) = 2 + 3 2 × 3 + 4 + 6 4 × 6 = 5 6 + 1 0 2 4 = 5 1 8 Ω