Circular arcs in a pentagon
An pentagon of side length is shown below. Five circular arcs are constructed on each side such that each arc passes through the two vertices of the side and such that it is tangent to the two other sides intersecting with that side. The arcs generate the shape of a flower with five petals with an overlap between them. Find the area of one petal excluding the overlap (the requested area is shaded in blue).
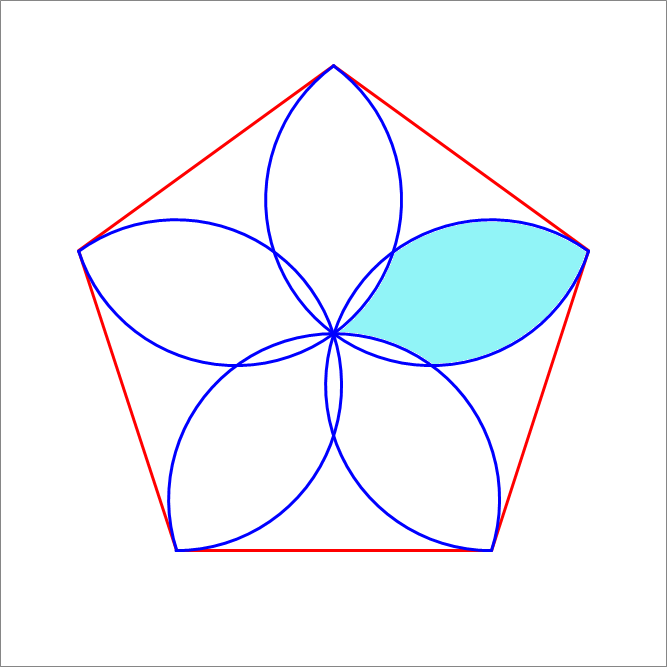
The answer is 0.942868444.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let O be the center point, C be the center of the top right circular arc, and A , B , D , and E be labelled as follows:
By symmetry, ∠ A O B = 5 3 6 0 ° = 7 2 ° , and since a central angle is twice the angle that subtends the same arc, ∠ A C B = 2 ⋅ 7 2 ° = 1 4 4 ° , which means ∠ B C D = 7 2 ° and ∠ B C O = 1 0 8 ° . Using trigonometry on right triangle △ B C D and using the given information that A B = 2 , B C = sin 7 2 ° 1 , and since B C is a radius, B C = C E = C O = sin 7 2 ° 1 .
Also by symmetry, ∠ C O E = 5 3 6 0 ° = 7 2 ° , and since △ C O E is an isosceles triangle, ∠ E C O = 3 6 ° .
The area of region between the line B O and arc B O is the difference between the area of the sector B C O and the triangle △ B C O , which is A B O = ( 3 6 0 ° 1 0 8 ° π − 2 1 sin 1 0 8 ° ) ( sin 7 2 ° 1 ) 2 , and similarly, A E O = ( 3 6 0 ° 3 6 ° π − 2 1 sin 3 6 ° ) ( sin 7 2 ° 1 ) 2 .
The desired area is then A P = 2 A B O − 4 A E O = 2 ( 3 6 0 ° 1 0 8 ° π − 2 1 sin 1 0 8 ° ) ( sin 7 2 ° 1 ) 2 − 4 ( 3 6 0 ° 3 6 ° π − 2 1 sin 3 6 ° ) ( sin 7 2 ° 1 ) 2 which simplifies to A P = ( 2 sin 3 6 ° − sin 1 0 8 ° + 5 1 π ) ( sin 7 2 ° 1 ) 2 . Substituting sin 3 6 ° = 4 1 0 − 2 5 and sin 7 2 ° = sin 1 0 8 ° = 4 1 0 + 2 5 further simplifies it to A P = ( 2 1 0 − 2 5 − 4 1 0 + 2 5 + 5 1 π ) ⋅ 1 0 + 2 5 1 6 ≈ 0 . 9 4 2 8 6 8 4 4 4 .