Circular arcs in an equilateral triangle
An equilateral triangle of side length is shown below. Three circular arcs are constructed on each side such that each arc passes through the two vertices of the side and such that it is tangent to the two other sides. The three arcs are also shown in the figure below. Find the area of the three petals resulting from this construction (shaded in orange).
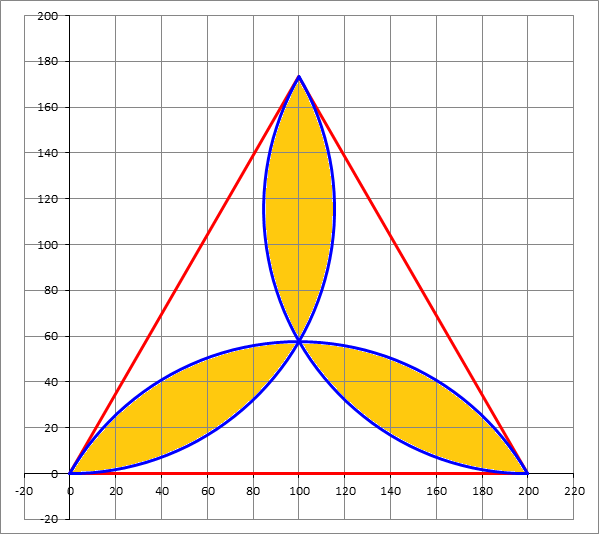
The answer is 7246.88.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We can tessellate this equilateral triangle to completely fill up the Cartesian plane. We can see that the area of the 3 petals is identical to 6 times the area of a segment of a circle, with radius r , and a central angle θ = 3 π .
The value of r can be solved using cosine rule , r 2 + r 2 − 2 r 2 ( 1 − cos ( 3 2 π ) ) = 2 0 0 2 ⇒ r 2 = 3 4 0 0 0 0 . Now, we use the formula of the area of a sector of a circle, 2 1 r 2 ( θ − sin θ ) = 9 1 0 0 0 0 ( 2 π − 3 3 ) . Multiply this value by 6 and we have our answer, 4 0 0 0 0 ( 3 π − 2 3 ) ≈ 7 2 4 6 . 8 8 5 .