Circular Cross Section of an Ellipsoid
An ellipsoid is given by 2 5 x 2 + 1 0 0 y 2 + 4 0 0 z 2 = 1 , and a plane containing the y -axis and making an angle of θ with the x y -plane cuts through the ellipsoid.
If the resulting intersection is a circle, find tan θ .
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
We can think of the circle of intersection as part of a sphere centered at the origin. Since the points with x = z = 0 , y = ± 1 0 lie on the ellipsoid and in the plane, they must be part of the circle, and therefore part of the sphere. Thus the sphere has radius 10. The circle is therefore (part of) the intersection of 2 5 x 2 + 1 0 0 y 2 + 4 0 0 z 2 = 1 and 1 0 0 x 2 + 1 0 0 y 2 + 1 0 0 z 2 = 1 . To solve this system, subtract the equations: 2 5 x 2 + 4 0 0 z 2 − 1 0 0 x 2 − 1 0 0 z 2 = 0 . Multiply everything by 100, and separate the variables: ( 4 − 1 ) x 2 = ( 1 − 4 1 ) z 2 ; 3 x = ± 2 1 3 z . It follows that tan θ = x z = ± 2 1 3 3 = ± 2 .
The equation of the plane is z = ± tan θ x , ( 0 < θ < 2 π ), and it intersects the ellipsoid in the x z -plane at a point that is 1 0 units from the origin. The intersection point satisfies,
2 5 x 2 + 4 0 0 z 2 = 1
Substituting for z ,
2 5 x 2 + tan 2 θ 4 0 0 x 2 = 1
Therefore,
x 2 = 1 6 + tan 2 θ 4 0 0
Now, we require the distance from the origin to be 1 0 , that is,
1 6 + tan 2 θ 4 0 0 + 4 0 0 tan 2 θ = 1 0 0
so that,
4 0 0 + 4 0 0 tan 2 θ = 1 6 0 0 + 1 0 0 tan 2 θ
and,
tan 2 θ = 3 0 0 1 2 0 0 = 4
Thus,
tan θ = 2
Note that we take only the positive root, because 0 < θ < 2 π .
A cross section of the ellipsoid and plane P with the x z -plane looks like: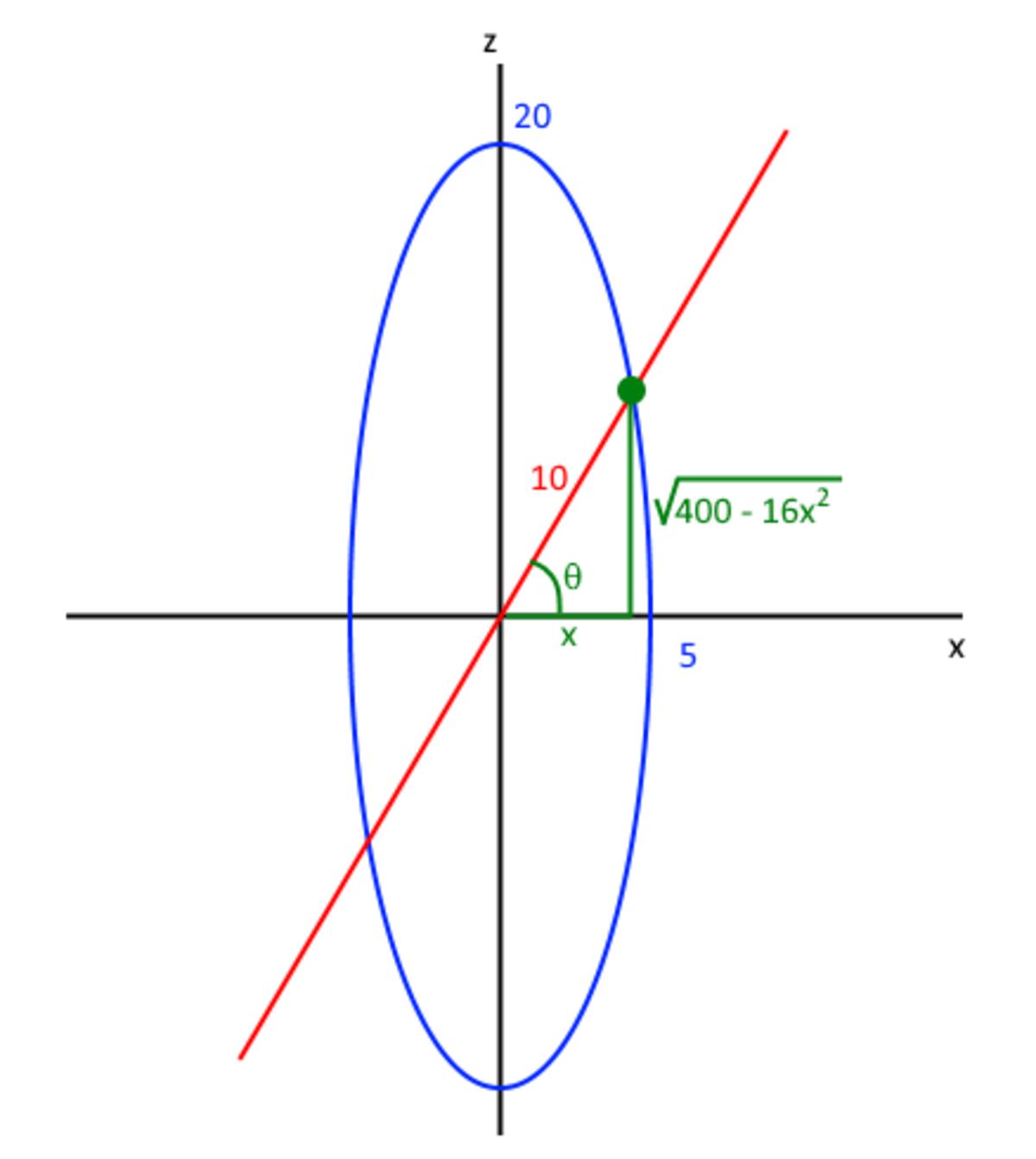 The portion of the red line inside of the blue ellipse contains the projection onto the
x
z
-plane of a circle of intersection between the ellipsoid and the plane
P
. This circle has radius 10 because it contains the points
(
0
,
±
1
0
,
0
)
on the diameter formed by the
y
-axis.
Use the Pythagorean theorem to find
x
, and then compute
tan
θ
.
The portion of the red line inside of the blue ellipse contains the projection onto the
x
z
-plane of a circle of intersection between the ellipsoid and the plane
P
. This circle has radius 10 because it contains the points
(
0
,
±
1
0
,
0
)
on the diameter formed by the
y
-axis.
Use the Pythagorean theorem to find
x
, and then compute
tan
θ
.