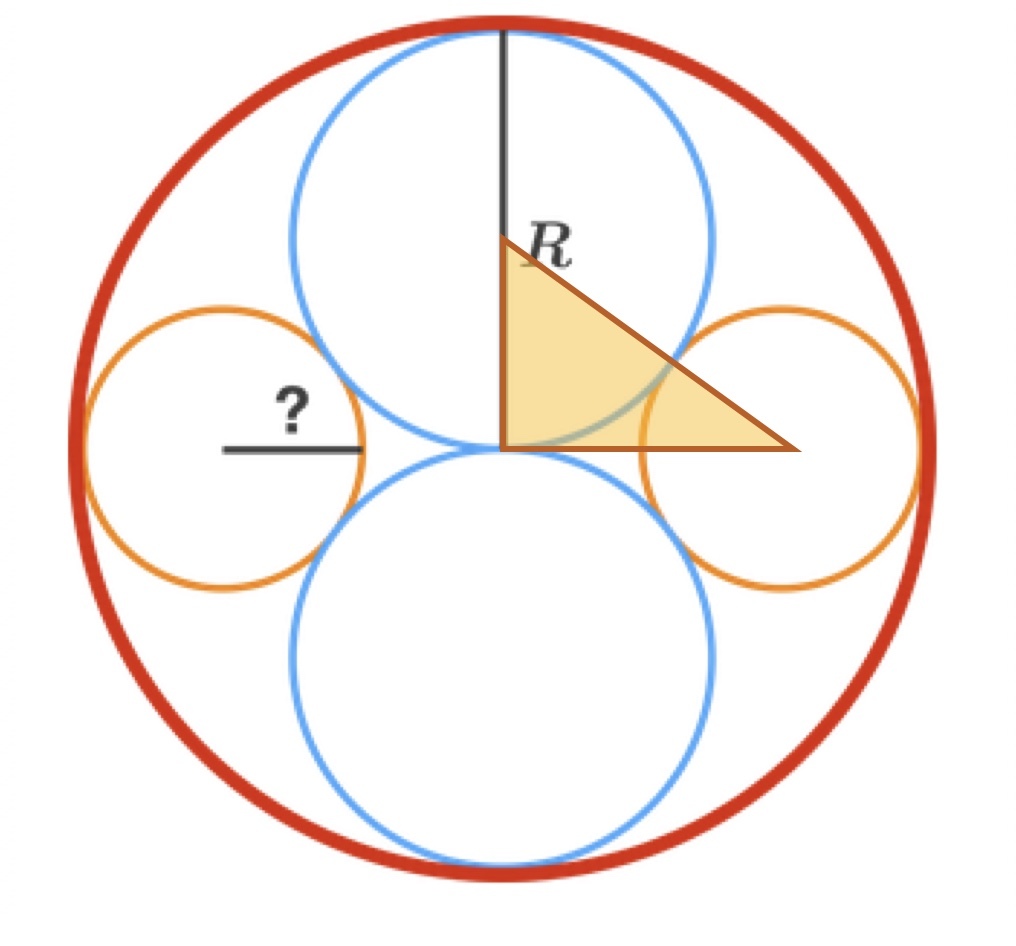
Circular Double Twins
There are two identical blue circles and two identical orange circles arranged symmetrically in a larger red circle, as shown. The circles are tangent to each other where they touch.
If the radius of the red circle is R , then what is the radius of one of the orange circles?
Hint : Try finding a right triangle and applying the Pythagorean theorem .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
how can O3c = R1 - R2???
Log in to reply
Because R1 in the red circle's radius and R2 is the orange circles radius. So by subtracting R2 from R1 we get that length which in R1 - R2.
I don't get how can R1-R2 = O3C?
Log in to reply
Because R1 in the red circle's radius and R2 is the orange circles radius. So by subtracting R2 from R1 we get that length which in R1 - R2.
Why O1C=O3C ?
Log in to reply
Because R1 in the red circle's radius and R2 is the orange circles radius. So by subtracting R2 from R1 we get that length which in R1 - R2.
How do you type fractions?
Log in to reply
He uses L a t e x . See the [ f o r m a t t i n g g u i d e ] ( h t t p s : / / b r i l l i a n t . o r g / m a t h − f o r m a t t i n g − g u i d e )
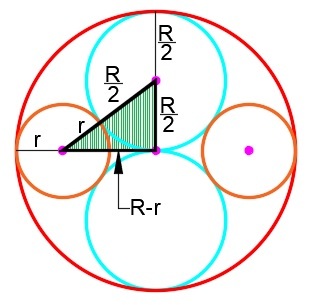
Let
r
be the unknown radius.
 The right triangle drawn here has horizontal leg
R
−
r
, vertical leg
2
1
R
, and hypotenuse
2
1
R
+
r
. Pythagoras says
(
R
−
r
)
2
+
(
2
1
R
)
2
=
(
2
1
R
+
r
)
2
.
R
2
−
2
R
r
+
r
2
+
4
1
R
2
=
4
1
R
2
+
R
r
+
r
2
.
Cancel the
r
2
, combine like terms, and divide by
R
to find
r
=
3
1
R
.
The right triangle drawn here has horizontal leg
R
−
r
, vertical leg
2
1
R
, and hypotenuse
2
1
R
+
r
. Pythagoras says
(
R
−
r
)
2
+
(
2
1
R
)
2
=
(
2
1
R
+
r
)
2
.
R
2
−
2
R
r
+
r
2
+
4
1
R
2
=
4
1
R
2
+
R
r
+
r
2
.
Cancel the
r
2
, combine like terms, and divide by
R
to find
r
=
3
1
R
.
I think you need to prove that the “hypotenuse” is indeed a straight line by pointing out that the orange circle radius and the blue circle radius are both perpendicular to the (same) tangent at the two circles’ intersection.
Log in to reply
Thanks for filling that gap... Yes, the two segments have the same direction because they are both perpendicular to the common tangent at their point of tangency.
Have you used the a^2+b^2=c^2 method? Where c is the hypotenuse? I have used that method and it works exactly the same way
Log in to reply
I did, with a = R − r , b = 2 1 R , and c = 2 1 R + r .
The large circle has a radius of
R
and the medium circles each have a radius of
2
R
. Then by
Descartes' Theorem
,
k
4
=
k
1
+
k
2
+
k
3
±
k
1
k
2
+
k
2
k
3
+
k
1
k
3
where
k
1
=
−
R
1
(the reciprocal of the radius of the large circle that is internally tangent to the others),
k
2
=
R
2
(the reciprocal of the radius of the medium circle that is externally tangent to the others), and
k
3
=
R
2
(the reciprocal of the radius of the medium circle that is externally tangent to the others).
Therefore,
k
4
=
−
R
1
+
R
2
+
R
2
±
−
R
1
R
2
+
R
2
R
2
−
R
1
R
2
=
R
3
, which makes the radius of the fourth smaller circle the reciprocal of
k
4
or
3
R
.
I like this alternative (non-Pythagorean) solution.
Yea sunce we have 4 circles mutually tangent, we can gauruntee this equation will get us a radius.
 2
R
=
r
a
d
i
u
s
o
f
t
h
e
b
l
u
e
c
i
r
c
l
e
and
r
=
r
a
d
i
u
s
o
f
t
h
e
o
r
a
n
g
e
c
i
r
c
l
e
2
R
=
r
a
d
i
u
s
o
f
t
h
e
b
l
u
e
c
i
r
c
l
e
and
r
=
r
a
d
i
u
s
o
f
t
h
e
o
r
a
n
g
e
c
i
r
c
l
e
Apply pythagorean theorem on the black right triangle,
( 2 R + r ) 2 = ( 2 R ) 2 + ( R − r ) 2
4 R 2 + 2 ( 2 R ) ( r ) + r 2 = 4 R 2 + R 2 − 2 R r + r 2
4 R 2 + R r + r 2 = 4 R 2 + R 2 − 2 R r + r 2
3 R r = R 2
r = 3 R
A clear and understandable engineering explanation. :-)
Create a triangle with sides: R - r, R/2 and R/2 + r and use Pythagoras. Little r stands for the radius of the smaller circle.
A very simple solution is rotating line R counterclockwise 90 degrees and seeing that the short line is 1/3 the radius
How can I prove that it’s third of R? We can create a right triangle that it’s height is R and the base is 2R. I am stuck in the step of “seeing” it is third of R.
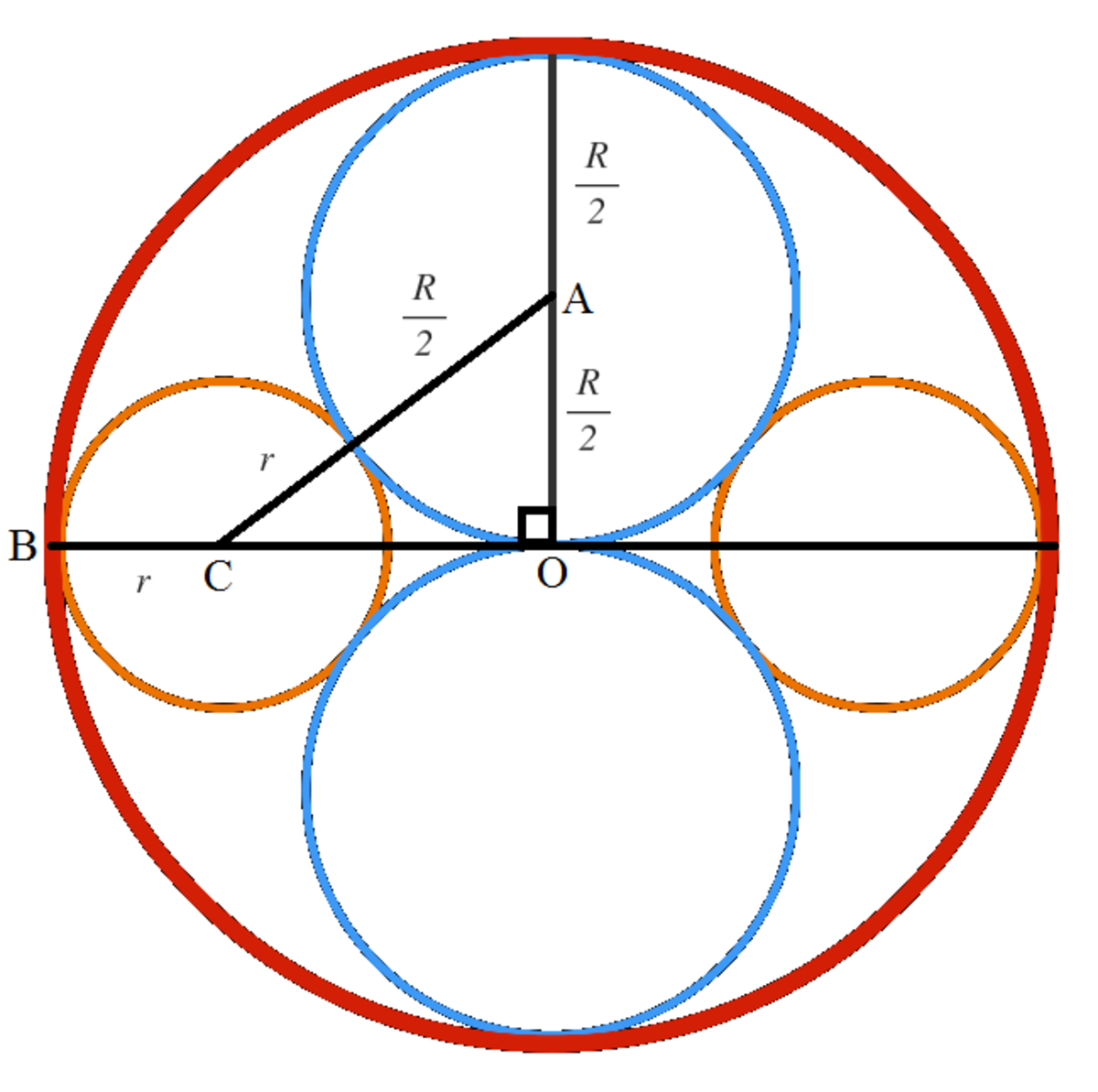 We note that the diameters of the blue circles and the extensions of the diameters of the orange circles meet at the center
O
of the big red circle. Let the radius of the orange circle be
r
. Since the radii
2
R
and
r
from the centers
A
and
C
of the top blue and the left orange circles respectively are perpendicular to their common tangent,
A
C
=
2
R
+
r
is a straight line. Now we have:
We note that the diameters of the blue circles and the extensions of the diameters of the orange circles meet at the center
O
of the big red circle. Let the radius of the orange circle be
r
. Since the radii
2
R
and
r
from the centers
A
and
C
of the top blue and the left orange circles respectively are perpendicular to their common tangent,
A
C
=
2
R
+
r
is a straight line. Now we have:
B C + C O r + A C 2 − A O 2 r + ( 2 R + r ) 2 − ( 2 R ) 2 ( 2 R + r ) 2 − ( 2 R ) 2 ( 2 R + r ) 2 − ( 2 R ) 2 4 R 2 + R r + r 2 − 4 R 2 3 R r ⟹ r = B O = R = R = R − r = R 2 − 2 R r + r 2 = R 2 − 2 R r + r 2 = R 2 = 3 R By Pythagorean theorem Squaring both sides
Well, everyobdy here have drawn the triangle, so watch it and read this. By using the hint: 4 R 2 + ( R − x ) 2 = ( 2 R + x ) 2 ⇒ 4 R 2 = ( 2 R + x + R − x ) ( 2 R + x − R + x ) ⇒ 6 R = 2 x − 2 R ⇒ x = 3 R
yeah we need to draw a triangle, the diagram is half of the solution . .
Log in to reply
And the difference is that...? You've seen the triangle, so you don't need me to draw it again
Solve this equation.
(R-x)² +(R/2)²= (X+(r/2))².
Where R is as given in question and x as the radius of smaller circle.
(Join the centres of all the circles. And then observe the right triangle formed)
(1st point- centre of largest circle
2nd point- centre of medium sized
Circle
3rd point- centre of smallest circle)
*All the above points are a part of the Rhombus formed in step 1
On solving the equation We get 4R² =12Rx On solving further x=R/3
Let the radius of the red circle be R 1 and the radius of the orange circle be R 2
Then we can find in the figure
O 3 O 1 = 2 R 1 + R 2
O 3 C = R 1 − R 2
O 1 C = 2 R 1
and we also see that O 3 C is tangent of both the blue circles. So ∠ O 1 C O 3 = 9 0 .
Therefore we can apply Pythagorean theorum for the right Δ O 1 C O 3
⇒ ( R 1 − R 2 ) 2 + ( 2 R 1 ) 2 = ( 2 R 1 + R 2 ) 2
⇒ R 1 2 + R 2 2 − 2 R 1 R 2 + 4 R 1 2 = 4 R 1 2 + R 2 2 + R 1 R 2
⇒ R 1 2 = 3 R 1 R 2
⇒ R 2 = 3 R 1