Circular Fractal Patters

Geometry Level 4

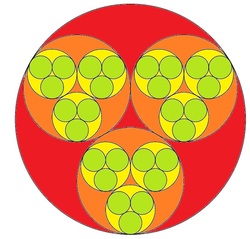Fractal Images are formed by geometrically repeating a pattern infinitely. Take for example the figure shown. Three smaller circles of equal radii are inscribed in a greater circle, where each smaller circle is tangent to the greater circle and the other two smaller circles. Then, each of the smaller circle circumscribes another set of even smaller circles of equal circles.

Let us say that the great circle drawn is a unit circle and we keep on drawing and drawing and drawing smaller circles following the pattern. What would the sum of the area of all the circles drawn in two decimal places?

The answer is 8.88.

3 solutions

Siddhant Pradhan
Mar 12, 2014

Consider one big circle with three smaller circles. if we join the centres of the three small circles, we see that the centre of the bigger circle is the centroid of that triangle. let C be centre of big circle and C1 be centre of any small circle. We have CC1+r=R by observation. For CC1 we use the above triangle. we shall get that CC1= (2/(sqrt3))r. Following this and solving we get [2(sqrt3)-3]R=r. This is now a Geometric Progression. But the trick was adding the increasing number of circles.. That's where my first attempt went wrong :p Cheers!

<DISCLAIMER:: Not able to reach the correct value at the end but the solution can be useful> Let r = radius of inner circles Then distance from center of one circle to center of other circles = 2r Equilateral triangle has side length 2r

Let x = distance from center of inner circles to center of larger circle x + r = R (radius of larger circle) We need to find x in terms of r, and then solve x + r = R to find r

To do so, we will use Law of cosines. As you can see from diagram, equilateral triangle can be divided into 3 smaller isosceles triangles with side lengths 2r, x, and x. The angle at the center of larger triangle (and at center of larger circle) is 360/3 = 120

Using law of cosines, we get: (2r)² = x² + x² - 2(x)(x) cos(120) 4r² = 2x² - 2x² * (-1/2) 4r² = 2x² + x² = 3x² x² = 4/3 r² x = 2/\sqrt{3} r

So, R=(2/\sqrt{3} +1)r

Ratio of 3 circles compared to the mother circle = 3*r^{2}/R^{2} If follow this series, 1+3(r/R)^{2}+9(r/R)^{4}...... =1/(1-3(r/R)^{2})=2.83

But, somewhere I am missing and not able to reach correct solution.

Anil Baratam - 7 years, 3 months ago

I did not use trignometry, but only used basic geometry and geometric progression to sum the areas.

I initially got the same exact answer as yours, but i found out where I went wrong, I assumed the great circle area as 1 instead of the radius as 1, i believe you did the same mistake as well, just multiply your answer by pi you get the correct answer.

I worked out the area as follows if A1 is the area of first bigger circle and A2, A3, are areas of subsequent smaller circles

Asum = A1 + 3A2 + 9A3 + 27A4 + ......

Radius, R2 = [ sqrt(3)/(2+sqrt(3)) ]* R1 and so on...

Then Asum = 8.8788426

John Samuel - 7 years, 3 months ago

Thanks!

Anil Baratam - 7 years, 3 months ago

from my study of ED we had a same problem in which 3 circles were inscribe in a big circle so i found that 45percent or so was the decrease in radius apply infinite GP sum to get result

Vishal Ch - 7 years, 2 months ago

Alfred Mark Aguilor
Mar 14, 2014

By using law of cosines, the radius of the first set of smaller circles is cos30/(1+cos30) = -3+2sqrt3. Let this value be "r".

The sum of the areas =pi+3pi(r^2)+9pi(r^4)+27pi(r^6)+... Since this is a geometric progression, this is equivalent to pi/(1-3(r^2)) = 8.8788.

Sreerag Rk
Apr 4, 2014

First Circle is having a radius of 1. At first we have to find the radius of first set of inner circle (3 circles inside the first larger circle).

Lines connecting the points at which the smaller circles touch the larger circle make an equilateral triangle having a side of sqrt(3).
In the same figure connect the centres of inner circles. It makes another equilateral triangle with one side equal to 2r1 (if r1 is the radius of the inner circle)
Centroid of both triangles coincides with the centre of the circle.
Length of the line connecting centre to vertex of outer triangle = 1 (radius of the larger circle).
Length of the line connecting centre to vertex of inner triangle = 1-r1.
From two similar triangles we can obtain the side of inner triangle = sqrt(3)x(1-r1)
i.e. 2r1 = sqrt(3) x (1-r1).
Solving this equation we get r1 = sqrt(3) / (2 + sqrt(3)).
If r2 is the radius of the second set of inner circles, r2 = {sqrt(3) / (2 + sqrt(3))} x r1
i.e. r2 = {sqrt(3) / (2 + sqrt(3))}^2
Similarly r3 = {sqrt(3) / (2 + sqrt(3))}^3 and so on....
Area of first circle = pi. r^2.
Total area of second three cirlces = 3 x pi x r1^2
Total area of third nine circles = 9 x pi x r2^2
Total area of all the circles drawn upto infinite times, A = pi. r^1 + 3pi. r1^2 + 9pi. r2^2 + .....
Substituting the values of r, r1, r2, r3,...... and taking pi outside from the total area, then A = pi. x (1 + 3{sqrt(3)/(2+sqrt(3))}^2 + 9{sqrt(3)/(2+sqrt(3))}^4 + 27{sqrt(3)/(2+sqrt(3))}^6 + ...... ) or A = pi. x S ------------------ eqn(1)
So S is the sum of a geometric series upto infinity with first term equal to '1' and common ratio equal to 3{sqrt(3)/(2+sqrt(3))}^2 (which is less than 1).
Sum of a GP upto infinity with common ration less than one is a/(1-r).
Therefore S = 1/[1- 3{sqrt(3)/(2+sqrt(3))}^2].
Substituting the value of S in eqn(1) and calculating the value upto two decimal places we get the value of A as 8.87 sq. units
Thus Sum of the areas of all the circles drawn is 8.87 sq. units.

Circular Fractal Patters

The answer is 8.88.

3 solutions

0 pending reports