Petals And Areas

Geometry Level 1

In the following diagram, the four small circles touch the boundary and center of the larger circle. The regions where, the smaller circles intersect one another are all equal.

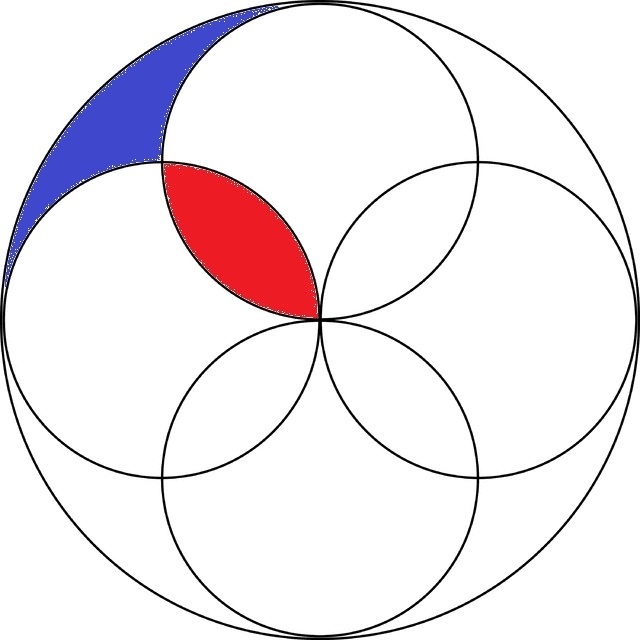
Find the ratio of the area of the blue region to the area of the red region.

1:1

1:2

2:3

3:2

1 solution

mR wisky sky zeRo
Jun 9, 2016

Relevant wiki: Length and Area - Composite Figures

let blue=A, red =B, and radius of large circle=R. $\pi R^2 - 4A= 4 \pi \left(\frac{R}{2}\right)^2 - 4B$ $\rightarrow A=B$

Petals And Areas

1 solution

0 pending reports