Circular orbit plane change (1)

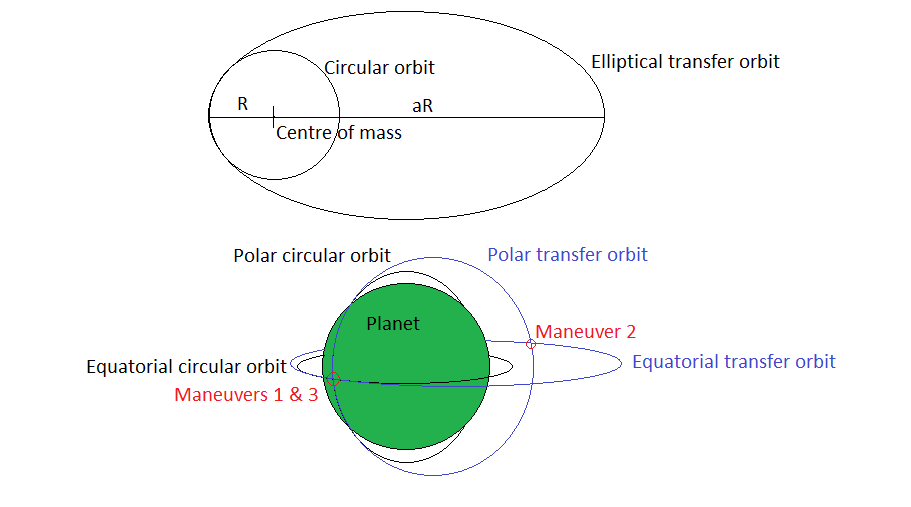
Your spacecraft is on an equatorial circular orbit (EO) around a spherical planet at $1\ \mathrm{km/s}$ relative to the center of the planet. You want to get to a polar orbit of same radius (PO, forming an angle of $\pi/2$ with the EO), yet the basic maneuver consisting of thrusting normally until you reach a polar orbit isn't the most efficient. For information, its required $\Delta v$ is $1.414\ \mathrm{km/s}$ .

Instead, you're going for a bi-elliptical transfer . Your flight plan is the following:

• Maneuver 1: Transfer from the EO to an equatorial transfer orbit .
• Maneuver 2: Plane change at apogee, now on a polar transfer orbit .
• Maneuver 3: Slowing down at perigee to reach the PO .

According to this procedure, what is the theoretical minimum $\Delta v$ required $($ in $\mathrm{km/s})?$