Circular Resistance?

Electricity and Magnetism Level 2

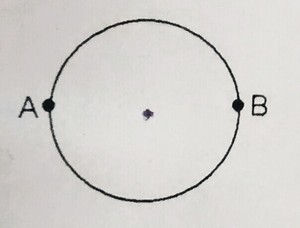
A wire of resistance 12 Ω / m 12\ \Omega/m is bent to form a complete circle of radius 10 cm \text{10 cm} as shown in the figure. What is the resistance between its two diametrically opposite points A A and B B ?

6 Ω 6\ Ω 6 π Ω 6 π\ Ω 3 Ω 3\ Ω 0.6 π Ω 0.6 π\ Ω

Aditya Shrivastava by Aditya Shrivastava , 17, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Max Yuen
Jun 3, 2019

The total resistance of the ring is R = ( 12 Ω / m ) × 2 π ( 0.1 m ) = 2.4 π Ω R=(12\Omega/m )\times 2\pi(0.1m) = 2.4\pi\Omega .

When the resistance is measured diametrically, it is equivalent to having the total resistance cut into two equal resistors with resistance equal to R / 2 R/2 but placed in parallel. Thus, the parallel resistance is equivalent to ( 1 R / 2 + 1 R / 2 ) − 1 = R / 4 = 0.6 π Ω \left(\frac{1}{R/2}+\frac{1}{R/2}\right)^{-1}=R/4 = 0.6\pi\Omega .

1 Helpful 0 Interesting 1 Brilliant 0 Confused

Can you please elaborate

Aditya Shrivastava - 2 years ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...