Circular Segment Party

Geometry Level 4

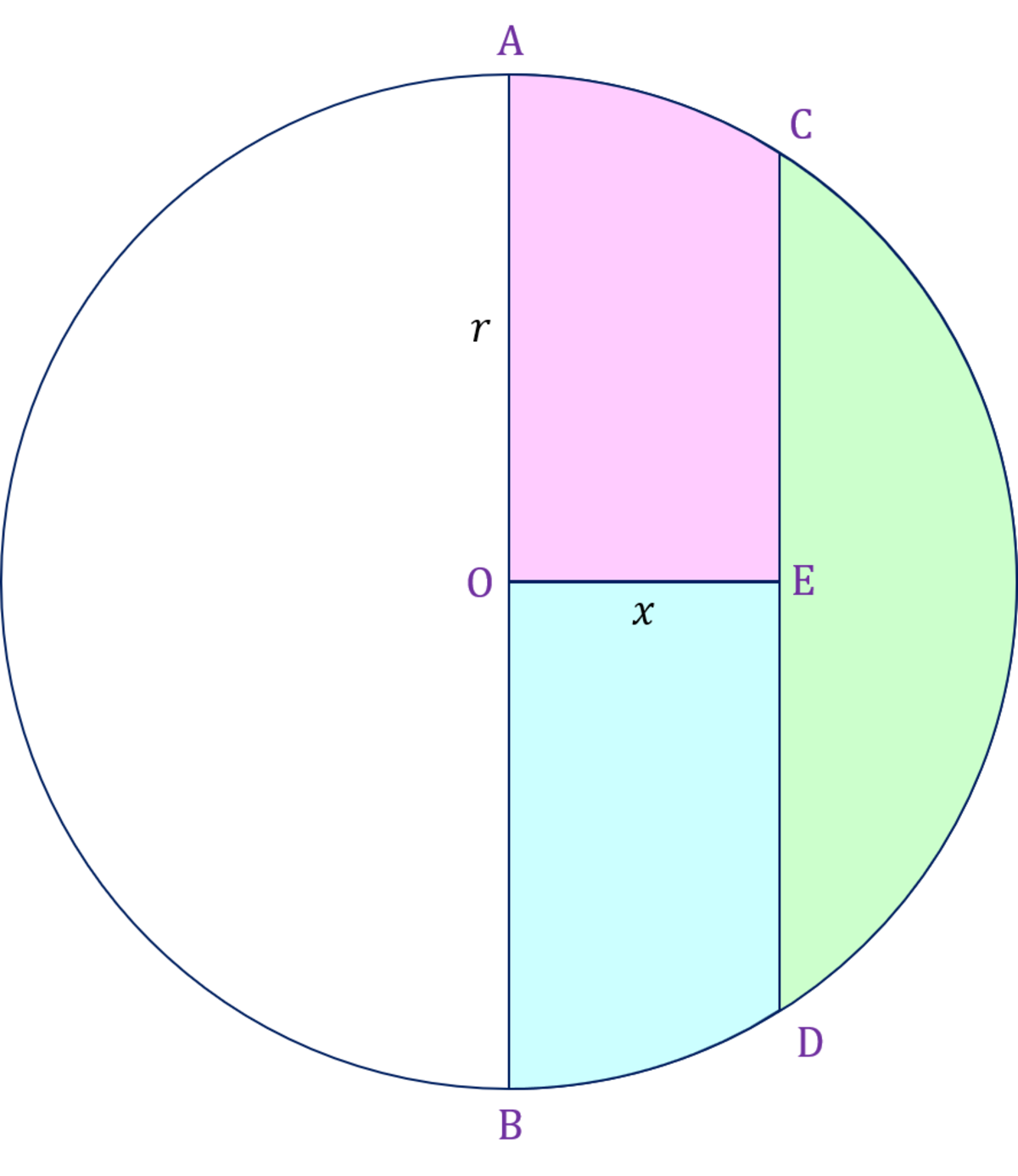
A circle centered at O O has a radius r r . The line A B ‾ \overline { AB } is the diameter of this circle and the line O E ‾ \overline { OE } is perpendicular with A B ‾ \overline { AB } . The line C D ‾ \overline { CD } is perpendicular with O E ‾ \overline { OE } and passes through point E E .

x x is the length of O E ‾ \overline { OE } that make the area of green area, pink area, and blue area equal.

Which of the following equation is correct?

x r 2 r 2 − x 2 + π 6 = arctan ⁡ r 2 − x 2 r \frac { x }{ { { r }^{ 2 } } } \sqrt { { r }^{ 2 }-{ x }^{ 2 } } +\frac { \pi }{ 6 } =\arctan ^{ }{ \frac { \sqrt { { r }^{ 2 }-{ x }^{ 2 } } }{ r } } x r 2 r 2 − x 2 + π 3 = arcsin ⁡ x r \frac { x }{ { { r }^{ 2 } } } \sqrt { { r }^{ 2 }-{ x }^{ 2 } } +\frac { \pi }{ 3 } =\arcsin { \frac { x }{ r } } x r 2 + x 2 = r 2 arccos ⁡ x r 2 + x 2 − π r 2 6 x\sqrt { { r }^{ 2 }+{ x }^{ 2 } } ={ r }^{ 2 }\arccos ^{ }{ \frac { x }{ \sqrt { { r }^{ 2 }+{ x }^{ 2 } } } } -\frac { \pi { r }^{ 2 } }{ 6 } x r 2 r 2 − x 2 = arcsin ⁡ r 2 − x 2 r − π 6 \frac { x }{ { { r }^{ 2 } } } \sqrt { { r }^{ 2 }-{ x }^{ 2 } } =\arcsin ^{ }{ \frac { \sqrt { { r }^{ 2 }-{ x }^{ 2 } } }{ r } } -\frac { \pi }{ 6 } x r = arccos ⁡ r r 2 + x 2 − π 3 \frac { x }{ { r } } =\arccos ^{ }{ \frac { r }{ \sqrt { { r }^{ 2 }+{ x }^{ 2 } } } } -\frac { \pi }{ 3 } x r 2 r 2 + x 2 + π 6 = arccos ⁡ x r \frac { x }{ { { r }^{ 2 } } } \sqrt { { r }^{ 2 }+{ x }^{ 2 } } +\frac { \pi }{ 6 } =\arccos ^{ }{ \frac { x }{ r } } r x 2 r 2 − x 2 = r 2 arccos ⁡ r 2 − x 2 r − π r 2 6 \frac { r }{ { { x }^{ 2 } } } \sqrt { { r }^{ 2 }-{ x }^{ 2 } } ={ r }^{ 2 }\arccos { \frac { \sqrt { { r }^{ 2 }-{ x }^{ 2 } } }{ r } } -\frac { \pi { r }^{ 2 } }{ 6 } x r 2 r 2 − x 2 = arccos ⁡ r x − π 6 \frac { x }{ { { r }^{ 2 } } } \sqrt { { r }^{ 2 }-{ x }^{ 2 } } =\arccos ^{ }{ \frac { r }{ x } } -\frac { \pi }{ 6 }

Sorawit Nick by Sorawit Nick , 18, Thailand

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

David Vreken
Mar 6, 2020

Draw C O CO and D O DO and let θ = ∠ C O E = ∠ D O E \theta = \angle COE = \angle DOE , let h = C E h = CE , and let A G A_G be the area of the green section.

Since the green, pink, and blue areas are equal, the green area is one third of half the circle, so A G = 1 6 π r 2 A_G = \frac{1}{6}\pi r^2 .

The green area is also the difference between the area of sector C O D COD and the area of △ C O D \triangle COD , so A G = 1 2 ⋅ 2 θ ⋅ r 2 − 1 2 ⋅ x ⋅ 2 h = θ r 2 − x h A_G = \frac{1}{2} \cdot 2\theta \cdot r^2 - \frac{1}{2} \cdot x \cdot 2h = \theta r^2 - xh .

Therefore, A G = 1 6 π r 2 = θ r 2 − x h A_G = \frac{1}{6}\pi r^2 = \theta r^2 - xh , which can be rearranged to x h r 2 = θ − π 6 \frac{xh}{r^2} = \theta - \frac{\pi}{6}

From right triangle △ C O E \triangle COE , since C O = r CO = r , O E = x OE = x , C E = h CE = h , and ∠ C O E = θ \angle COE = \theta , by trigonometry h = r 2 − x 2 h = \sqrt{r^2 - x^2} and θ = arcsin ⁡ r 2 − x 2 x \theta = \arcsin \frac{\sqrt{r^2 - x^2}}{x} .

Substituting these into x h r 2 = θ − π 6 \frac{xh}{r^2} = \theta - \frac{\pi}{6} gives x r 2 r 2 − x 2 = arcsin ⁡ r 2 − x 2 x − π 6 \boxed{\frac{x}{r^2}\sqrt{r^2 - x^2} = \arcsin \frac{\sqrt{r^2 - x^2}}{x} - \frac{\pi}{6}}

1 Helpful 1 Interesting 0 Brilliant 0 Confused

may be coe = arc sin h/r

trupal panchal - 1 year, 3 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...