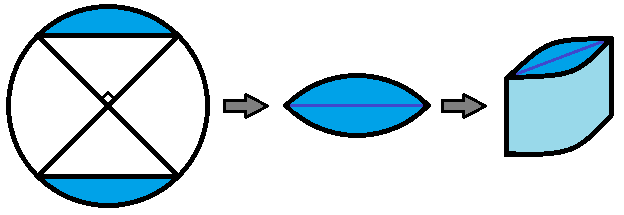
Circular Segments Container

Let $r$ =radius, $h$ =height, $S$ =surface area, $V$ =Volume

The area of the two segments combined is $2 \cdot ( \frac{\pi r^{2}}{4} -\frac{r^{2}}{2})=(\frac{\pi}{2}-1)r^{2}$ and so $V=(\frac{\pi}{2}-1)r^{2}h$

Since $V$ is fixed let's cleverly set $V=\frac{\pi}{2}-1$ so that $r^{2}h=1$ or $h=\frac{1}{r^2}$

$S=2(\frac{\pi}{2}-1)r^{2}+\pi r h$ but making the above substitution gives $S$ as a function of $r$ :

$S(r)=(\pi-2)r^{2}+\frac{\pi}{r}$ [A quick graph tells us the minimum around $r=1.1$ will easily be found using the derivative.]

$S'(r)=(2\pi-4)r-\frac{\pi}{r^{2}}=0$

$(2\pi-4)r=\frac{\pi}{r^{2}}$

$r^{3}=\frac{\pi}{2\pi-4}$ [The cube root of this is around 1.1 but it turns out we don't need it.]

We are told to find $\frac{h}{r}$ but we can substitute $h=\frac{1}{r^{2}}$ to get $\frac{1}{r^{3}}$ which is just the reciprocal of the above $r^{3}$

So the ratio is $\frac{2\pi-4}{\pi}=2-\frac{4}{\pi}$ . This means $a=2$ and $b=4$ so the solution is $a+b=\boxed{6}$