Circular Train Track
There are 10 stations on a circular path. A train has to stop at 3 stations such that no two stations are adjacent. How many such selections are possible?
The answer is 50.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
Why do we fix 7 stations ?
Log in to reply
Because we are considering only 3 stations. 10-3=7.
Did the same!
Quite creative!!!
Log in to reply
Why don't you post a similar solution to the 100 side polygon question.
Log in to reply
Yeah the solution from 100 side polygon question was pretty informative
First of all,the number of ways in which 3 stations can be chosen from 1 0 = ( 3 1 0 ) .Now,if we subtract from this:the cases in which the train stops at two adjacent stations but not at three adjacent stations and the cases in which the train stops at three adjacent stations,we would have our answer.Let us count the number of ways in which the train stops at three consecutive stations, ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ 1 , 2 , 3 2 , 3 , 4 3 , 4 , 5 . . . . . . 9 , 1 0 , 1 1 0 , 1 , 2 .That is a total of 1 0 cases.Now,moving on to the second case,number of ways of choosing 2 consecutive stations but not three consecutive stations as that has already been counted. ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ 1 , 2 2 , 3 3 , 4 . . . . . . 9 , 1 0 1 0 , 1 .That is a total of 1 0 ways.But we have only selected 2 stations,for the third one:let us take the first case, 1 , 2 now that we have selected 1 and 2 we can't select 3 and neither can we select 1 0 .Thus,we have to choose from 6 stations.Thus,for each of the 1 0 cases we have 6 choices.Total = 6 0 .Thus,answer = ( 3 1 0 ) − 7 0 = 5 0 .
Same method. Easy and no complications
Did the exact same . Nice and easy.
thanks..really nice solution
Did the same
Label the stations 1 through 10 going clockwise, and assume that the starting point of the train is between stations 10 and 1. So going clockwise, the train will pass a stations before making its first stop, b stations before making its second, c stations before making its third stop and d stations before crossing its starting point, where
(i) b , c are positive integers,
(ii) a , d are non-negative integers, at least one of which is a positive integer, and
(iii) a + b + c + d = 7 , as 1 0 − 3 = 7 stations are passed over in total.
Condition (ii) is required since stations 1 and 10 are adjacent, (since the path is circular), and thus we cannot have a = d = 0 .
This problem can be solved using the stars and bars method. We then need to look at the following cases:
- a = 0 , d > 0 : equation (iii) then becomes b + c + d = 7 with each of b , c , d being positive integers, which according to Theorem 1 of the link has
( 3 − 1 7 − 1 ) = ( 2 6 ) = 1 5 solutions.
-
a > 0 , d = 0 : by symmetry, this will yield the same result of 1 5 solutions.
-
a > 0 , d > 0 : equation (iii) then becomes a + b + c + d = 7 with each of a , b , c , d being positive integers, which according to Theorem 1 has
( 4 − 1 7 − 1 ) = ( 3 6 ) = 2 0 solutions.
So in total the number of suitable station selections is 1 5 + 1 5 + 2 0 = 5 0 .
I thought 1 , 3 , 5 was different from 3 , 1 , 5 .
The formula is 1 0 × ( 2 × 5 + 5 × 4 ) ÷ 6 .
- 1 0 for the first station, where there are ten choices.
- Now we divide it into two cases, one in which the second station is directly two stations away from the first station, and the other in which the second station is more than two stations away from the first station.
- There are 2 ways to choose a station that is directly two stations away.
- If such a station is chosen, the third station would have 5 choices left.
- There are 5 ways to choose a station that is more than two stations away from the first station.
- If such a station is chosen, the third station would have 4 choices left.
- Divide by 6 because the order of the three stations does not matter, so each combination is overcounted by a factor of 3 ! = 6 .
We will use 2nd Kaplansky's Lemma which states that The number of ways of selecting k objects, no two consecutive,from n objects arrayed in a circle is n − k n ( k n − k )
Here n = 1 0 , k = 3
Answer= 7 1 0 ( 3 7 ) = 5 0 .
NOTE:This was just to produce an alternative solution.Memorizing any formula like this is never recommended in combinatorics problem
Do such questions using Gautam's or charlesworth's method posted here
Moderator note:
What is the explanation of the formula?
While I agree that memorization of formula shouldn't be encouraged, the main point is for you to understand how it was obtained, so that you can reproduce it in such a scenario.
Well, how come you wrote ( n − k n ) but substituted as ( 3 7 ) ?
I think you could modify Gautam's argument to get the formula. Arrange the stations/gaps in a circular fashion, fixing the first on the top. So you have (7 choose 3) gap choices. Do it for every station, so multiply by 10. In the circle every station was overselected (7 times more), so divide by 7. In general, replace 10 by n , 3 by k and 7 by n − k .
Take three number in ascending order a , b , c which represent the number of stations. If we transform it into the couple a , b + 1 , c + 2 we will be almost sure that there is no pair of the closest stations. So, since we have 1 0 stations we have to be sure that a > = 1 and c + 2 < = 1 0 . Therefore, we can choose ( 3 8 ) .
However, if we have the pair a = 1 , d = 8 than we have close stations 1 and 1 0 . Therefore, we have to exclude all of them. Using the same logic we can see that we can chose from the range 8 > = b + 1 > = 3 therfore, b ∈ [ 2 ; 7 ] and the total number of such quadrilaterals is ( 1 6 ) .
The answer is ( 3 8 ) − ( 1 6 ) = 5 0
Using your solution of this question I have solved many level 4 question thank you very much for sharing this.
First choose 3 stations in 10c3 ways. Here,we have included the cases where all 3 stations are adjacent as well as the case where 2 of them are adjacent and the other one is not.So we have to subtract these cases. Now 3 adjacent stations are {s1,s2,s3},{s2,s3,s4},....{s9,s10,s1},{s10,s1,s2}...(where s1,s2....s10 are the 10 stations) Which gives us 10 For the second case of 2 adjacent and and third station non adjacent,2 adjacent can again be chosen in 10 ways but the non adjacent can be chosen only in 6 ways(suppose s3,s4 are the adjacent ones then for the third station, s2,s3,s4,s5 cannot be chosen as it should be adjacent. Which gives us 10.6 (for 10.6 the reason is fundamental principle of multiplication Therefore required answer=10c3-(10+10.6) =120-70 =50 Note:this can also be solved by using the formula for selecting p objects with no two adjacent out of n objects arranged in a circle, which is n/(n-p) * (n-p)cp Cheers!
The number of selections is equal to the number of triangles such that none of their vertices are adjacent. By PIE, the number of such triangles is equal to ( 3 1 0 ) − 1 0 ⋅ 8 + 1 0 = 5 0
A basic thinking without any named lemma and formula:
All the possibility including 1: 1,3,5-9 (5 solution) +1,4,6-9 (4 solution) etc. So altogether 5+4+3+2+1=15 solution. 1 was chosen here random, so it is true for any station, this means 10X15 solution, but we counted every solution three times (at every station), so the solution is 150/3= 50
Well, I just directly used this: nC3-n(n-4)-n Put n=10 for ans.
Can you elaborate on your answer?
Log in to reply
I guess he has interpreted the question as no of triangles that can be formed with no side of decagon in common. That's a good way to solve it.
Log in to reply
Essentially the same thing as Adarsh Kumar's and my similar solution..

Using gap method we fix 7 stations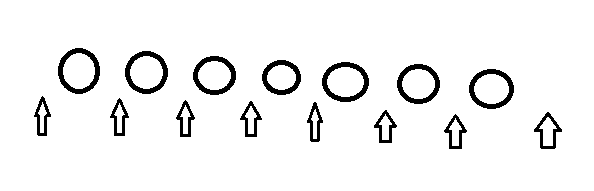 .
.
Arrows shows gaps and circles stations.
Now chosing 3 arrows from 8 (no one will be adjacent) But when when we chose first and last and form a circle then two stations will be adjacent which is possible by ->6 ways (third arrow six places left) Hence 8 C 3 − 6 = 5 0