Circulators
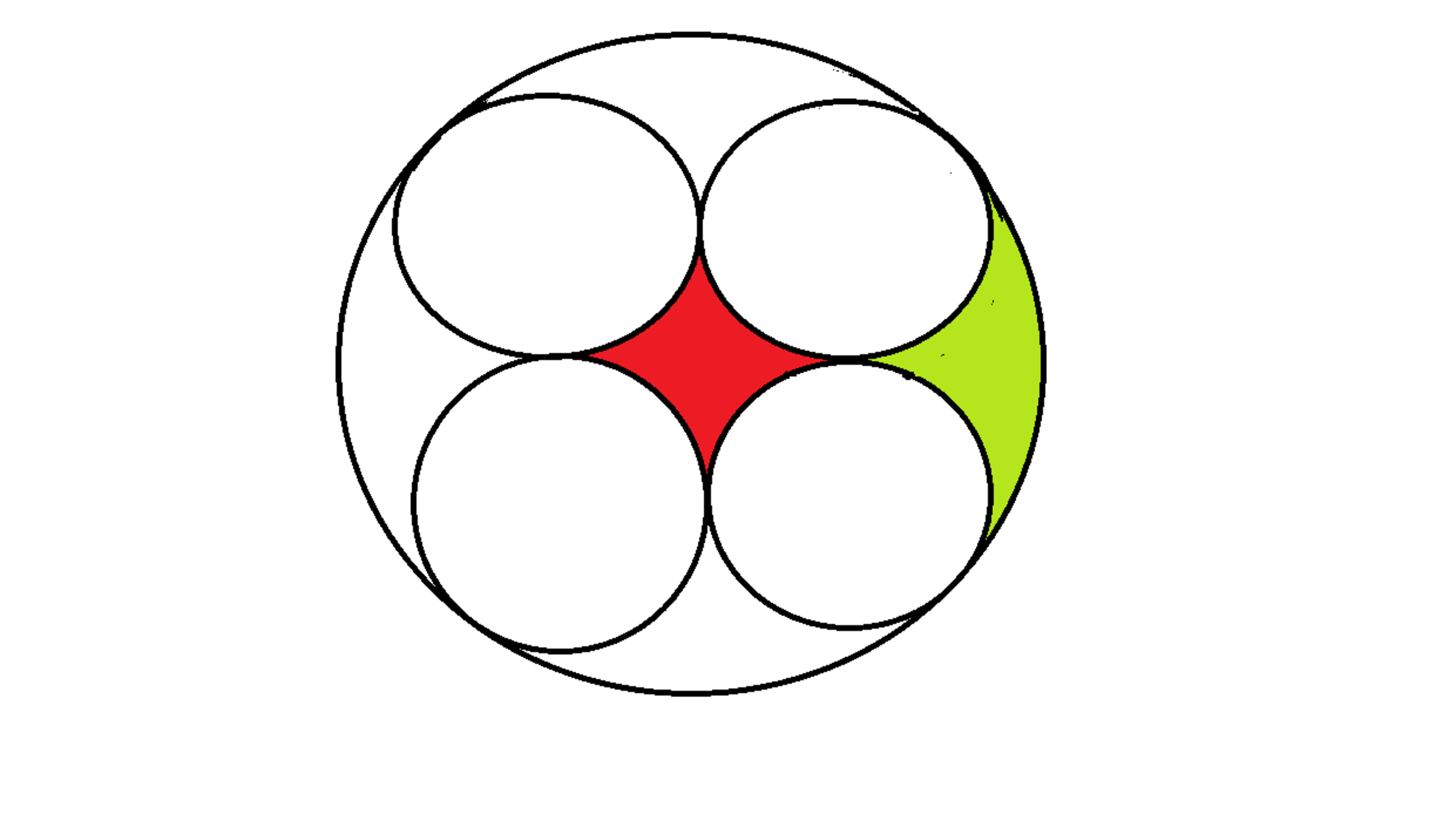
Four unit circles are inscribed inside a larger circle as shown on the figure provided. if the area of the red region is M and that of the green region is N , then :
= ?
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The centres of the four unit circles form four vertices of a square of side-length 2 , and the diagonal of the square = 2√2 . The radius of the larger circle = (2√2 + 2)/2 = √2 + 1.
Af = area which is inside larger circle but out side the four unit circles = π { ( √2 + 1 ) ² - 4 } = 2√2π – π.
M = area of square – 4 quarter unit circles = 4 – π.
4N = Af - M = 2√2π – π – 4 + π = 2√2π – 4.
N = π/√2 -1.
N + 1 = π/√2.
Hence answer is 4 .