Circumcenter Cevians Take 2
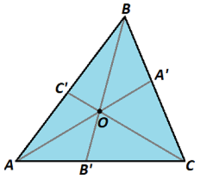
If △ A B C has cevians A A ′ = 2 6 2 7 9 2 6 , B B ′ = 2 4 2 1 1 6 , and C C ′ = 2 2 3 2 3 1 7 4 through its circumcenter O , then find its area.
The answer is 336.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Nice solution! I believe there's a typo, though, it should say, "we deduce that R = 4 6 5 ". (The R value is corrected later on when it is put into your B coordinates.)
I use
2. ExactTrilinearCoordinates.html
and I find formula for length for the cevians, and find lengths sides of triangle by Mathcad. And after I use HeronsFormula .
Let r = A O = B O = C O . Since an inscribed angle is half of a central angle that subtends the same arc, ∠ B O C = 2 A , so ∠ B O C ′ = ∠ C O B ′ = 1 8 0 ° − 2 A (from the straight line), and ∠ C B O = ∠ B C O = 9 0 ° − A (from the isosceles triangle △ B O C ). Similarly, ∠ A O C ′ = ∠ C O A ′ = 1 8 0 ° − 2 B and ∠ A O B ′ = ∠ B O A ′ = 1 8 0 ° − 2 C , and ∠ A C O = ∠ C A O = 9 0 ° − B and ∠ A B O = ∠ B A O = 9 0 ° − C . Using the law of sines on △ B O A ′ gives O A ′ = cos ( B − C ) r cos A . Similarly, O B ′ = cos ( A − C ) r cos B and O C ′ = cos ( A − B ) r cos C . Therefore, A A ′ = A O + O A ′ = r + cos ( B − C ) r cos A = r ( 1 + sin B sin C + cos B cos C cos A ) . Similarly, B B ′ = r ( 1 + sin A sin C + cos A cos C cos B ) and C C ′ = r ( 1 + sin A sin B + cos A cos B cos C ) .
Using the theorem A A ′ 1 + B B ′ 1 + C C ′ 1 = r 2 (see theorem and proof here ) and the given values for A A ′ , B B ′ , and C C ′ , r solves to r = 4 6 5 .
Letting x = cos A , y = cos B , then sin A = 1 − x 2 and sin B = 1 − y 2 , and cos C = cos ( 1 8 0 ° − ( A + B ) ) = − cos ( A + B ) = sin A sin B − cos A cos B = ( 1 − x 2 ) ( 1 − y 2 ) − x y and sin C = sin ( 1 8 0 ° − ( A + B ) ) = sin ( A + B ) = sin A cos B + cos A sin B = y 1 − x 2 + x 1 − y 2 .
Substituting these values in the A A ′ and B B ′ equations gives:
A A ′ = 2 7 9 7 2 8 0 = 4 6 5 ( 1 + 1 − y 2 ( y 1 − x 2 + x 1 − y 2 ) + y ( ( 1 − x 2 ) ( 1 − y 2 ) − x y ) x )
B B ′ = 2 1 5 2 0 = 4 6 5 ( 1 + 1 − x 2 ( y 1 − x 2 + x 1 − y 2 ) + x ( ( 1 − x 2 ) ( 1 − y 2 ) − x y ) y )
which has two solutions ( x , y ) = ( − 5 3 , − 6 5 3 3 ) and ( x , y ) = ( 5 3 , 6 5 3 3 ) . However, ( x , y ) = ( − 5 3 , − 6 5 3 3 ) gives two obtuse angles for ∠ A and ∠ B , which is not possible, so ( x , y ) = ( 5 3 , 6 5 3 3 ) .
Using these values x = 5 3 and y = 6 5 3 3 gives sin A = 1 − x 2 = 1 − ( 5 3 ) 2 = 5 4 , sin B = 1 − y 2 = 1 − ( 6 5 3 3 ) 2 = 6 5 5 6 , and sin C = y 1 − x 2 + x ( 1 − y 2 ) = 6 5 3 3 1 − ( 5 3 ) 2 + 5 3 ( 1 − ( 6 5 3 3 ) 2 ) = 1 3 1 2 .
Therefore, the area of △ A B C = 2 r 2 sin A sin B sin C = 2 ⋅ ( 4 6 5 ) 2 ⋅ 5 4 ⋅ 6 5 5 6 ⋅ 1 3 1 2 = 3 3 6 .
I don't have a solution, but just for the record, the sides of the triangle are B C = 2 6 , A C = 2 8 , and A B = 3 0 .
..which means that A B C is a 1 0 , 2 4 , 2 6 ) right-angled triangle stuck together with a 1 8 , 2 4 , 3 0 ) right-angled triangle. We can choose coordinates A ( − 1 0 , 0 ) , B ( 0 , 2 4 ) and C ( 1 8 , 0 ) , obtaining the outcentre at 4 , 4 3 3 ) and solving easy simultaneous equations to obtain, for example, B ’ ( 2 1 1 2 8 , 0 ) and C ’ ( 3 2 3 3 0 4 2 , 3 2 3 3 6 9 0 ) , and so on. I would still like to find a more elegant derivation than mine!
Log in to reply
Yes, those triangle sides are correct and those are the two right-angled triangles I combined to make the problem. I basically solved the problem by forcing two cevians to be expressed in terms of x = cos A and y = cos B , but the equations were messy.
If R is the outradius, define u = A A 1 − R and v = B B 1 − R .
Set up a coordinate system with the triangle outcentre at the origin, and with B having coordinates ( − R , 0 ) . Then B 1 has coordinates ( v , 0 ) , and A and C both lie on a straight line through B 1 . Without loss of generality, we can assume that A lies above the x -axis, and so that ∠ A O B 1 = θ lies between 0 and π . Then A and C are the points of intersection of the circle and line x 2 + y 2 = R 2 y = tan θ ( x − u ) and hence we have coordinates A C ( v sin 2 θ + cos θ R 2 − v 2 sin 2 θ , − v sin θ cos θ + sin θ R 2 − v 2 sin 2 θ ) ( v sin 2 θ − cos θ R 2 − v 2 sin 2 θ , − v sin θ cos θ − sin θ R 2 − v 2 sin 2 θ ) and A 1 will have coordinates A 1 ( − R u ( v sin 2 θ + cos θ R 2 − v 2 sin 2 θ ) , − R u ( − v sin θ cos θ + sin θ R 2 − v 2 sin 2 θ ) ) and from this it follows that B , A 1 and C will be collinear precisely when R ( R + u ) v cos θ + ( R 2 − R u − 2 u v ) R 2 − v 2 sin 2 θ = 0 ( ⋆ ) It is a fairly standard result that A A 1 1 + B B 1 1 + C C 1 1 = R 2 where R is the outradius. With A A 1 = 2 6 2 7 9 2 6 , B B 1 = 2 4 2 1 1 6 and C C 1 = 2 2 3 2 3 2 2 4 we deduce that R = 4 6 5 . Putting t = tan 2 1 θ , the equation ( ⋆ ) squares to give 0 = 3 9 6 9 t 4 − 8 9 6 2 t 2 + 3 9 6 9 = ( 7 t − 9 ) ( 7 t + 9 ) ( 9 t − 7 ) ( 9 t + 7 ) Since 0 < θ < π , we have t = 9 7 or 7 9 . It turns out that only t = 9 7 is a proper solution of ( ⋆ ) --- the other solution is introduced by the squaring process, and so we deduce that we have coordinates A ( 5 2 5 9 5 , 1 3 1 5 0 ) B ( − 4 6 5 , 0 ) C ( 2 0 9 1 , − 5 7 8 ) which makes the area of the triangle equal to 3 3 6 .