Circumcenter On Circumcircle

Geometry Level 4

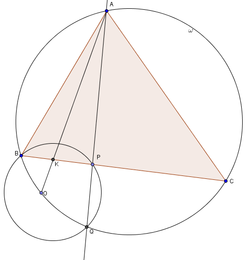Let $\omega$ be the circumcircle of a triangle $\triangle ABC.$ A line $\ell$ passing through point $A$ intersects segment $BC$ and $\omega$ at points $P,Q$ respectively (where $Q \neq A$ ). Let $O$ be the circumcenter of $\triangle BPQ,$ and let $AO$ intersect $BC$ at $K.$ Given that $O$ lies on $\omega,$ find $\angle AKB$ in degrees.

Note: The image is not drawn to scale.

The answer is 90.

2 solutions

Nguyen Thanh Long
Apr 15, 2014

$BO=QO \Rightarrow \angle{BAO}=\angle{QAO}$ $BO=PO \Rightarrow BP \perp AO$ $\angle{AKB}=\boxed{90^{o}}$

Why does BO=PO necessiate BP perp tp AO?It could be at some other angle also.?

Amit Chopra - 7 years, 1 month ago

Because $A$ and $O$ both lie on the perpendicular bisector of $AP.$

Sreejato Bhattacharya - 7 years, 1 month ago

Actually arcs BO = QO since they are cut on on w at equal distances from O.Hence <BAO =<QAO.But both of these are angles lying on both sides of AO which is the line joining the centre of the smaller circle to O.Hence Arc BP is divided into two equal arcs at point of intersection with AO.Hence <BOk=<KOP.Thus triangles BOK and KOP are congruend due to SAS criterion since BO = OP beind the radii.Hence <BKO =<OKP each of which are right angles as they are a linear pair.

Amit Chopra - 7 years, 1 month ago

Why doesn't my full comment show?Please advise.

Amit Chopra - 7 years, 1 month ago

Aaaaa Bbbbb
Apr 24, 2014

Call O' is circumcenter of ABC. $\angle{OO'Q}=\angle{CBQ} => \angle{BO'O}=\angle{OO'Q} => \angle{BAO}=\angle{OAQ}$ $\triangle{BAO}=\triangle{QAO} => \angle{AKB}=\boxed{90^{0}}$

Circumcenter On Circumcircle

The answer is 90.

2 solutions

0 pending reports