Circumcircle and Tangents

$\text{Since ABC is a right triangle, the circumcenter is the midpoint of the hypotenuse (using Thale's theorem)}$

By the alternate segment theorem , all the angles having the same color are equal to each other. Also,

$AB = 10 \cos\left(\frac {\pi}{12}\right), BC = 10 \sin\left(\frac {\pi}{12}\right)$

Using the law of sines we have -

$BF = \frac {BC \cdot \sin(\frac {\pi}{12})}{\sin(\frac {5\pi}{6})} , BE = \frac {AB \cdot \sin (\frac {5\pi}{12})}{\sin(\frac {\pi}{6})}$

Since $OB = 5$ , substituting in values we get $[\triangle OEF]$ = $[\triangle OFB]$ + $[\triangle OEB]$ = $\frac {5}{2}(BF+BE) = \dfrac{5}{2} \left(\dfrac{10\sin^2(\frac {\pi}{12})}{\sin(\frac {5\pi}{6})} + \dfrac {10\cos(\frac {\pi}{12}) \cdot \sin(\frac {5\pi}{12})}{\sin(\frac {\pi}{6})}\right) = \boxed {50}$

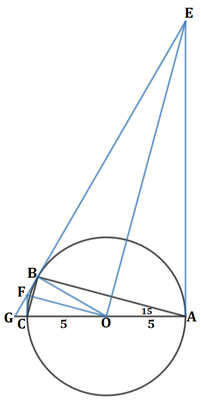
Since $\triangle ABC$ is a right triangle, the circumcenter $O$ is at the midpoint of $CA$ , so that the radius is $CO = OA = OB = 5$ .

$\triangle OBA$ is an isosceles triangle, so if $\angle BAC = 15°$ then $\angle OBA = 15°$ , which means $\angle BOA = 180° - 15° - 15° = 150°$ .

Since $\angle OBE = \angle OAE = 90°$ , $OBEA$ is a cyclical quadrilateral, which means $\angle BEA = 180° - \angle BOA = 180° - 150° = 30°$ .

By alternate interior angles of parallel segments $FC || EA$ , $\angle GFC = \angle BEA = 30°$ .

Since $\angle GFC = \angle BEA = 30°$ , $GF = 2GC$ and $GE = 2GA$ .

Since $GE = GF + FE$ and $GA = GC + CA$ , by substitution, $GE = 2GC + FE = 2GA = 2GC + 2CA$ , so that $FE = 2CA = 2 \cdot 10 = 20$ .

Therefore, $\triangle OEF$ has a base of $FE = 20$ and a height of $OB = 5$ , so its area is $\frac{1}{2} \cdot 20 \cdot 5 = \boxed{50}$ .