Circumcircle of equilateral triangle
What is the area of an equilateral triangle if the area of its circumcircle has the same numeric value as its side length?
If your answer is in the form c π 2 a b , where b is square-free and a and c are relatively prime, find a + b + c .
The answer is 16.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let the side lengths of the equilateral triangle be a .
We can drop a perpendicular bisector from any one of the vertices and this would split the triangle into two congruent right triangles, with hypotenuse of length a , and a leg with length 2 a . By Pythagoras' theorem, the second leg has a length of 4 4 a 2 − a 2 = 2 a 3 . This is the altitude of any equilateral triangle with side length a . But since the triangle is equilateral, we know that this is also the median, and so the circumradius is the distance from the circumcenter to each vertex, but also the distance from the centroid to each vertex (since the centroid and circumcenter are the same point, in this case).
The distance from any vertex to the centroid is two thirds the length of the median, and so the circumradius is 3 2 ⋅ 2 a 3 = a 3 3 = 3 a .
So the area of the circumcircle is π ( 3 a ) 2 = 3 1 π a 2 . Since this is equal to the side length of the triangle, we set this equal to a and get:
3 1 π a 2 = a ⟹ a = π 3 . The area of the equilateral triangle in terms of a is 2 1 ⋅ a ⋅ 2 a 3 = 4 a 2 3 .
As such, we see that the area of the triangle is ( π 3 ) 2 4 3 = 4 π 2 9 3 .
Hence, a + b + c = 9 + 3 + 4 = 1 6 .
If the radius of the circumcircle is r , then the side length of the equilateral triangle will be s = 3 r , and its area will be 4 3 s 2 = 4 3 3 r 2 .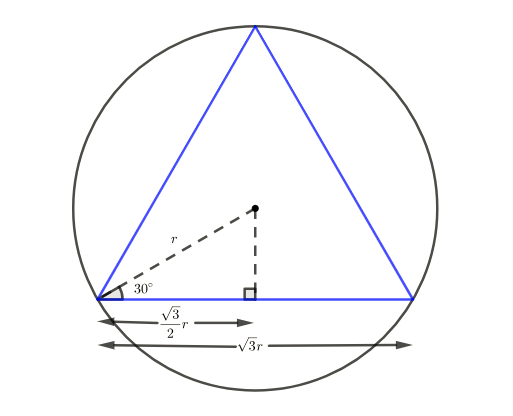
The condition in the question translates to π r 2 = 3 r , i.e. r = π 3 .
Then the area of the equilateral triangle is 4 3 3 r 2 = 4 3 3 ( π 3 ) 2 = 4 π 2 9 3 = c π 2 a b , so the answer is a + b + c = 9 + 3 + 4 = 1 6