Circumcircle to four unit circles
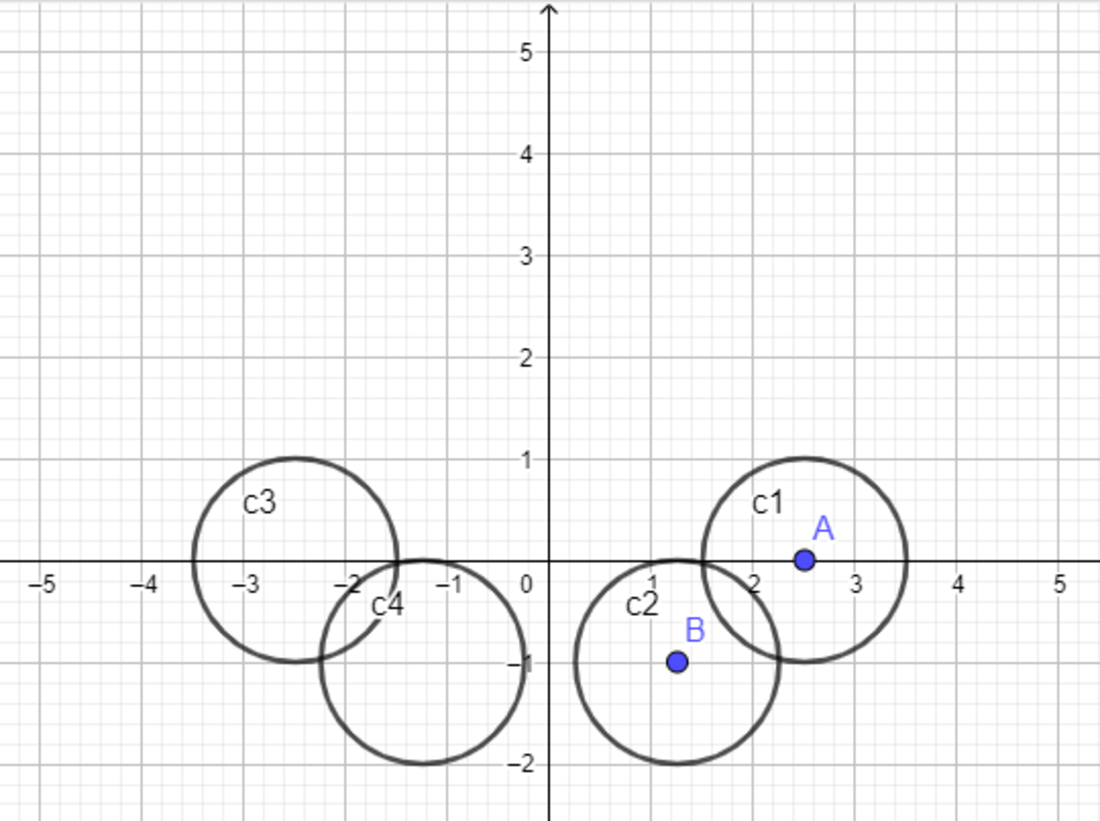
As shown in the figure, you are given a unit circle centered at , and unit circle centered at . You also have circles and which are reflections of and about the -axis. Find the radius of the circumscribed circle that is tangent to all four circles and has them inside it, and submit
The answer is 4106.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
As the system is symmetrical about the y -axis, we can expect that the center of the circle tangent to the four circles lies on the y -axis. Let the center be P ( 0 , y 0 ) . Since the P is equidistance from the circumferences of the four circles, it must also be equidistance from the four centers. As the system is symmetrical about the y -axis, we need only to consider one side and I am choosing C 1 and C 2 and we have:
( 2 5 ) 2 + y 0 2 4 2 5 ⟹ y 0 = ( 4 5 ) 2 + ( y 0 + 1 ) 2 = 1 6 2 5 + 2 y 0 + 1 = 3 2 5 9
Then the radius of the circle tangent internally to the four circles is R = A P + 1 = ( 2 5 ) 2 + ( 3 2 5 9 ) 2 + 1 ≈ 4 . 1 0 6 3 5 0 6 0 1 9 9 ⟹ ⌊ 1 0 0 0 R ⌋ = 4 1 0 6 .